Семинар-5
Методом динамического программирования решить следующую задачу:
Задача. Поиск оптимального пути между двумя пунктами.
Решение:
1. Для простоты допустим, что прокладка пути состоит из ряда шагов, и на каждом шаге мы можем двигаться либо строго на восток, либо строго на север; любой путь из А в В представляет собой ступенчатую ломаную линию, отрезки которой параллельны одной из координатных осей.
2.Разделим расстояние от А до В в восточном направлении, например, на 7 частей, а в северном -- на 5 частей. Тогда любой путь из А в В состоит из m = 5 + 7 = 12 отрезков, направленных на во-ток или на север. Проставим на каждом из отрезков число, выражающее стоимость прокладки пути по этому отрезку. Требуется выбрать такой путь из А в В, для которого сумма чисел, стоящих на отрезках, минимальна.
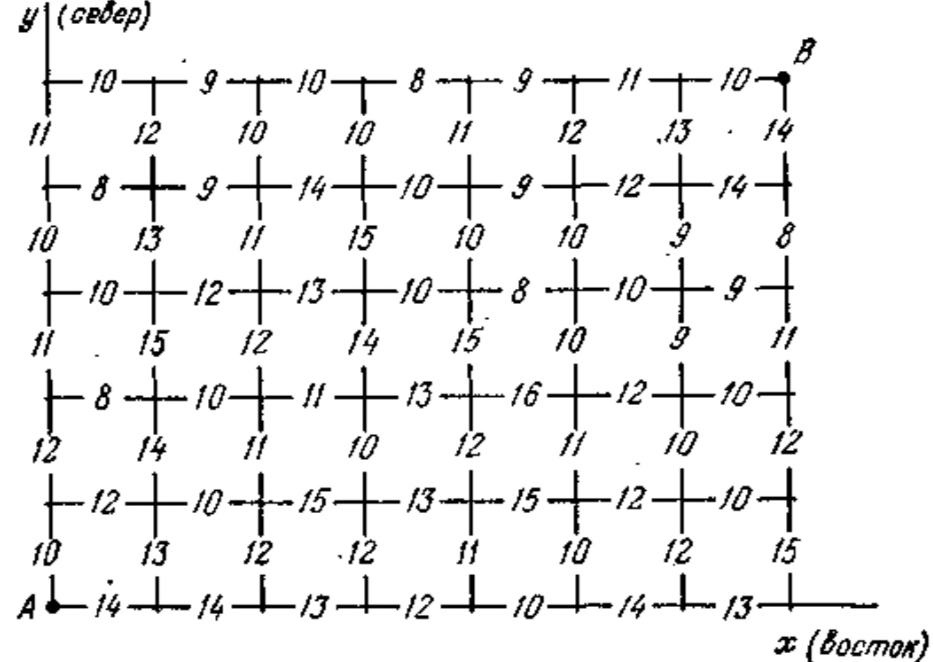
3. Будем рассматривать сооружаемый путь как управляемую систему S, перемещающуюся под влиянием управления из начального состояния А в конечное В. Состояние этой системы перед началом каждого шага будет характеризоваться двумя координатами: восточной (х) и северной (у), обе -- целочисленные (0 ≤ х ≤ ≤ 7, 0 ≤ y ≤ 5). Для каждого из состояний системы (узловой точки прямоугольной сетки на рисунке) мы должны найти условное оптимальное управление: идти нам из этой точки на север (управление «с») или на восток (управление «в»). Выбирается это управление так, чтобы стоимость всех оставшихся до конца шагов (включая данный) была минимальна. Эту стоимость мы будем называть «условным оптимальным выигрышем» для данного состояния системы S перед началом очередного шага.
4. Процедуру условной оптимизации будем разворачивать в обратном направлении -- от конца к началу. Прежде всего произведем условную оптимизацию последнего, 12-го шага. Рассмотрим отдельно правый верхний угол нашей прямоугольной сетки.
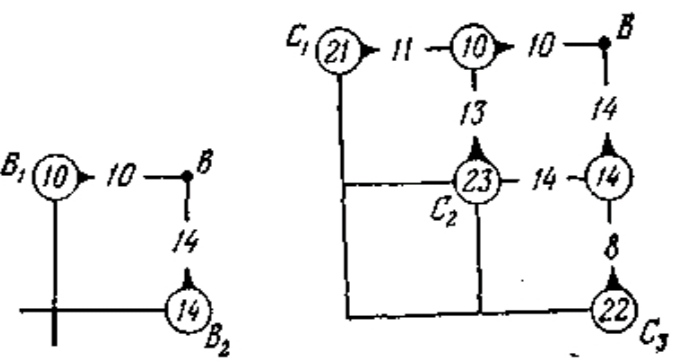
После 11-го шага можем находиться только там, откуда за один (последний) шаг можно попасть в В, т. е. в одной из точек В1 или В2. Если мы находимся в точке В1, у нас нет выбора (управление вынужденное): надо идти на восток, и это обойдется нам в 10 единиц. Запишем это число 10 в кружке у точки В1, а оптимальное управление покажем короткой стрелкой, исходящей из В1 и направленной на восток. Для точки B2 управление тоже вынужденное (север), расход до конца равен 14, мы его запишем в кружке у точки В2. Таким образом, условная оптимизация последнего шага сделана, и условный оптимальный выигрыш для каждой В1, В2 найден и записан в соответствующем кружке. Теперь давайте оптимизировать предпоследний (11-й) шаг. После предпоследнего (10-го) шага мы могли оказаться в одной из точек С1, С2, С3 (см. рис. выше). Найдем для каждой из них условное оптимальное управление и условный оптимальный выигрыш. Для точки С1 управление вынужденное: идти на восток; обойдется это нам до конца в 21 единицу (11 на данном шаге, плюс 10, записанных в кружке при Bi). Число 21 записываем в кружке при точке С1. Для точки С2 управление уже не вынужденное: мы можем идти как на восток, так и на север. В первом случае мы затратим на данном шаге 14 единиц и от В2 до конца -- еще 14, всего 28 единиц. Если пойдем на север, затратим 13 + 10, всего 23 единицы. Значит, условное оптимальное управление в точке С2 -- идти на север (отмечаем это стрелкой, а число 23 записываем в кружке у С2). Для точки С3 управление снова вынужденное («с»), обойдется это до конца в 22 единицы (ставим стрелку на север, число 22 записываем в кружке при С3).
5. Аналогично, «пятясь» от предпоследнего шага назад, найдем для каждой точки с целочисленными координатами условное оптимальное управление («с» или «в»), которое обозначим стрелкой, и условный оптимальный выигрыш (расход до конца пути), который запишем в кружке. Вычисляется он так: расход на данном шаге складывается с уже оптимизированным расходом, записанным в кружке, куда ведет стрелка. Таким образом, на каждом шаге мы оптимизируем только этот шаг, а следующие за ним -- уже оптимизированы.
6. Таким образом, условная оптимизация уже выполнена: в какой бы из узловых точек мы ни находились, мы уже знаем, куда идти (стрелка) и во что нам обойдется путь до конца (число в кружке). В кружке при точке А записан оптимальный выигрыш на все сооружение пути из А в В: W* = 118. Теперь остается построить безусловное оптимальное управление -- траекторию, ведущую из А и В самым дешевым способом. Для этого нужно только «слушаться стрелок», т. е. прочитать, что они предписывают делать на каждом шаге. Такая оптимальная траектория отмечается дважды обведенными кружками. Соответствующее безусловное оптимальное управление будет: x*=(c, c, c, c, в, в, с, в, в, в, в, в) т. е. первые четыре шага мы должны делать на север, следующие два -- на восток, затем опять один на север и остальные пять -- на восток. Задача решена.