Лабораторная работа 4
Задание:
- Разработать алгоритм моделирования СМО M|M|1|0
- Получить выборочных характеристик СМО и выполнить анализ полученных результатов.
Пусть λ — интенсивность простейшего потока требований, µ
— параметр распределения времени обслуживания. Если в момент прихода требования в систему
прибор свободен, то требование немедленно начинает обслуживаться. Если же прибор занят, то
требование покидает систему необслуженным. В момент t = 0 прибор свободен.
Рассматриваемая СМО описывается случайным процессом N(t) — числом требований в
системе или числом занятых приборов в момент времени t. N(t) есть цепь Маркова с множеством
состояний 0, 1 и с вероятностями переходов:
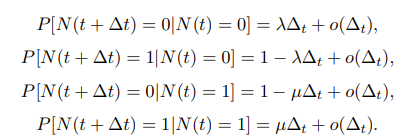
N(t) — регенерирующий случайный процесс, точками регенерации которого являются моменты начала (или окончания) обслуживания требований.
Стационарные вероятности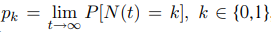 
существуют при всех положительных λ и µ:
Обозначения:
τi — момент поступления в СМО i–го требования, 0 = τ0 < τ1 < τ2 < . . . ;
ti = τi − τi−1 — интервал между моментами поступления в СМО (i − 1)–го и i–го требования.
Так как
входящий поток требований является простейшим, то случайные величины ti независимы и распределены по показательному закону с параметром λ;
xi — возможная длительность обслуживания i–го требования в предположении, что это требование не было потеряно; {xi} есть последовательность независимых случайных величин, распределенных по показательному закону с параметром µ;
Реализация Xi = (ti
, xi
, ∆i) описывает процесс функционирования СМО.
Значения {∆i} получаются при помощи следующего алгоритма:
0). β0 ≡ 0; i = 0; 1.
1) i = i + 1;
2) Если τi ≥ βi−1, то ∆i = 1, βi = τi + xi ; если τi < βi−1, то ∆i = 0, βi = βi−1;
3) Если i < n, то переход на 1. Далее в последовательности ∆i отбрасываем повторяющиеся значения (первые из каждого повтора оставляем), в результате чего получаем строго возрастающую последовательность ∆∗ 0 = 0 < ∆∗ 1 < ∆∗ 2 < . . . < ∆∗ n моментов окончания обслуживания требований и {N(∆∗ k ), k ≥ 0} есть регенеративный процесс.
Задание 1. Реализовать описанный алгоритм, получить точечные оценки стационарных вероятностей (3.11) и построить соответствующие доверительные интервалы. Исследовать, как эти доверительные интервалы накрывают значения параметров (3.11) в зависимости от уровня значимости γ и числа циклов регенерации n.
Задание 2. Построить оценки Биля, Филлера, Тина и ”складного ножа“ вместе с соответствующими доверительными интервалами; сравнить полученные результаты с классической оценкой в
виде отношения средних (3.2) из задания 1.
Теоретический материал к лабораторной работе
Процесс имитационного моделирования состоит из трех последовательно выполняемых этапов:
1. Строится математическая модель СМО;
2. Функционирование этой модели воспроизводится на вычислительном устройстве при помощи соответствующих алгоритмов
3. Результаты этих экспериментов обрабатываются статистическими методами, что позволяет
сделать необходимые выводы об интересующих характеристиках исследуемого объекта.
Имитационные модели предназначаются для:
— статистического оценивания параметров, характеризующих работу СМО;
— проверки статистических гипотез относительно параметров этих СМО; — оптимизации режима функционирования СМО;
— проверки точности численного анализа СМО и т. д. Эти имитационные модели должны обеспечивать указанные свыше возможности при следующих условиях: — при различных способах формирования входящего потока требований и при различных видах зависимости во входящем потоке требований;
— при различных дисциплинах обслуживания требований;
— при различных видах зависимости между фрагментами механизма обслуживания требований и т. д.
Для осуществления моделирования необходимы исходные данные, которые подразделяются на:
— исходные данные, позволяющие выбрать конкретную модель СМО;
— исходные данные, задающие характеристики входного потока и механизма обслуживания;
— исходные данные, задающие конкретные значения параметров СМО;
— уровень значимости, который должен быть достигнут при моделировании и т. д.
Воспроизведение процесса функционирования СМО на вычислительном устройстве фактически состоит в получении вектора состояний системы в какие-то дискретные моменты времени τi , i ≥ 0. При моделировании как правило задается начальное состояние системы (сети) в момент τ0, а затем согласно принятой математической модели разыгрываются последующие состояния в моменты τ1, τ2, . . . . Строится траектория вектора состояний системы в интервалах [τ0, τ1), [τ1, τ2), [τ2, τ3) и т. д.
Моменты τ1, τ2, . . . могут выбираться двумя способами.
Первый из них, называемый способом ”∆τ“, состоит в том, что моменты τ1, τ2, . . . являются неслучайными и τi − τi−1 = ∆τ, i ≥ 1, где ∆τ — некоторый заранее выбранный интервал, такой, что возможностью более чем одного изменения вектора состояний системы за время ∆τ можно пренебречь. Тогда по имеющемуся вектору состояний в момент τi случайным образом имитируется возможный переход в другое состояние за время ∆τ (отметим, что этого перехода может и не быть), и в результате получается вектор состояний в момент τi+1. Описанный способ выбора моментов τi обладает как достоинствами, так и недостатками. Достоинства заключаются в простоте реализации процесса моделирования. Недостатки проявляются в следующем. При слишком больших ∆τ результаты имитационного моделирования не адекватно аппроксимируют траекторию вектора состояний системы, а при слишком малых ∆τ требуются значительные затраты машинного времени, так как на каждое изменение вектора состояний требуется большое число имитаций.
Второй способ выбора моментов τi , называемый способом ”особых состояний“, состоит в том, что значения τi являются случайными, моделируются на вычислительном устройстве и при этом обладают тем свойством, что вектор состояний системы изменяется лишь в моменты τi , причем изменяется лишь одна компонента этого вектора, а в промежутке (τi , τi−1) изменений не происходит. Поэтому при таком моделировании системы (сети) достаточно лишь следить за ее особыми состояниями, что позволяет значительно уменьшить затраты машинного времени по сравнению с первым способом выбора моментов τi . Алгоритм моделирования способом ”особых состояний“ отличается от процедуры моделирования способом ”∆τ“ лишь тем, что требуется специальный алгоритм моделирования интервалов τi–τi−1. К тому же здесь не возникает проблемы выбора ”оптимального“ значения ∆τ . После того как получена реализация вектора состояний системы, необходимо обработать имеющиеся данные методами математической статистики. Проблемы, возникающие на этом этапе, заключаются в следующем.
Во-первых, в большинстве случаев оцениванию подлежат стационарные характеристики систем и, если учитывать данные с момента начала моделирования, то сказывается влияние начального заполнения системы. Поэтому возникает вопрос о длительности ”периода стабилизации“, т. е. до какого момента данные моделирования не следует учитывать, а с какого — принимать во внимание.
Во-вторых, практически всегда данные являются сильно коррелированными. По таким данным хотя и можно построить точечную оценку интересующего параметра, но не удается построить
соответствующий доверительный интервал с заданным уровнем значимости. Это связано с тем, что
теория доверительного оценивания использует, как правило, совокупности независимых и одинаково распределенных случайных величин из некоторого распределения вероятностей.
Пусть исследуется немарковская однолинейная СМО и необходимо оценить W — среднее время ожидания в стационарном режиме. Использование имитационного моделирования в этой задаче является естественным,
так как отсутствуют простые в вычислительном отношении аналитические результаты для точного
определения необходимой характеристики.
Обозначим ωk — время ожидания начала обслуживания k–м требованием. Состоятельной
оценкой математического ожидания случайной величины является выборочное среднее и в нашем
случае в качестве оценки для W будем использовать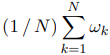 
где N — число требований, сгенерированных входящим потоком за время моделирования. Но выписанная оценка в силу влияния
начального заполнения системы будет в общем случае смещенной, так как если, например, ω1 = 0,
то и последующие несколько значений ωk будут малыми. К тому же, если для какого–то k–го требования время ожидания ωk велико, то и несколько последующих требований будут иметь большие
времена ожидания. Все это говорит о том, что последовательность случайных величин {ωk, k ≥ 1}
является коррелированной, что создает трудности при обработке результатов наблюдений.
Необходимо отметить, что ряд процессов, описывающих поведение отдельных характеристик систем (сетей) МО, обладает определенным свойством, а именно свойством регенерации, что
дает возможность использовать специальную методику обработки результатов наблюдений над такими процессами, преодолевающую отмеченные трудности.
Определение 1. Последовательность случайных величин {ξn, n = 0, 1, 2, . . .} является процессом восстановления, если ξ0 = 0 и {ξn − ξn−1, n ≥ 1} есть независимые, одинаково распределенные неотрицательные величины.
Определение 2. Последовательность {X(n), n ≥ 1} случайных векторов называется регенерирующим процессом, если существует последовательность 1 ≤ β1 < β2 < β3 < . . . случайных дискретных моментов времени, являющихся процессом восстановления, такая, что ∀ k > 0 и для любой другой последовательности моментов времени 0 < n1 < n2 < . . . < nm (m ≥ 1) случайные векторы {X(n1), X(n2), . . . , X(n − m)} и {X(n1 + βk), X(n2 + βk), . . . , X(nm + βk)} имеют одинаковое распределение, а процессы {X(n), n < βk} и {X(p), p > βk} являются независимыми. Моменты времени {βk, k ≥ 0} назовем точками (моментами) регенерации процесса Xn, случайную величину αk = βk+1 −βk назовем k–м периодом регенерации, а часть процесса {X(n), βk ≤ n < βk+1} будем называть k–м циклом.
Многие процессы, описывающие функционирование СМО и СеМО, являются
регенерирующими. В однолинейных стационарных СМО с обслуживанием типа GI регенерирующими являются такие процессы, как число требований в системе в момент времени t,
время ожидания n–го требования и виртуальное время ожидания в момент времени t. Для первого процесса точками регенерации являются номера требований с нулевым временем ожидания, а
для двух последующих процессов — моменты начала периодов занятости. В таких системах циклы
регенерации совпадают с периодами занятости.
В экспоненциальных СеМО регенерирующим является векторный случайный процесс X(t),
компоненты которого равны числу требований в узлах обслуживания в момент времени t. Точками
регенерации в рассматриваемом случае являются моменты возвращения процесса X(t) в некоторое
заранее фиксированное состояние.
Из введенных определений следует, что последовательность периодов регенерации {αk, k ≥
1} состоит из независимых и одинаково распределенных случайных величин. Аналогичное утверждение справедливо и для последовательности циклов регенерационного процесса. Если теперь
результаты моделирования сгруппировать по циклам, то получившиеся выборки будут независимы и одинаково распределены, что позволяет наряду с оценками средних значений интересующих параметров указать и соответствующие доверительные интервалы. Методика такого построения в
общем виде следующая.
Пусть имеется реализация X(t), 1 ≤ t ≤ N, некоторого регенерирующего процесса и по ней
необходимо построить точечную оценку и соответствующий доверительный интервал для параметра θ = E[X(t)], представляющего собой какую–то характеристику системы, функционирующей в
стационарном режиме. Считаем, что за время моделирования N сгенерировалось n периодов регенерации, и для простоты предположим, что первый цикл регенерации начался в самом начале
моделирования, а n–й цикл закончился в момент N, т. е. β1 = 1 и βn = N.
Известно, что состоятельной оценкой математического ожидания является выборочное среднее. Поэтому оценку параметра запишем в виде:
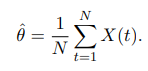
Обозначим:
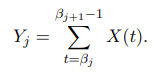
Так как: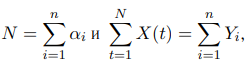 
то имеет место представление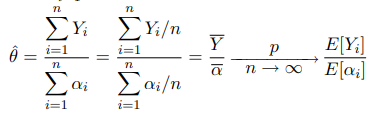 
в силу закона больших чисел при достаточно общих условиях на распределения циклов и периодов
регенерации. Обозначим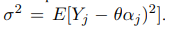 
Так как из определения регенерирующего процесса
следует, что последовательность {(Yj , αj ), 1 ≤ j ≤ n} состоит из независимых и одинаково распределенных случайных векторов, то в силу центральной предельной теоремы при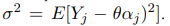 
для
статистики
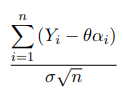
имеет место асимптотическая при n → ∞ нормальность:
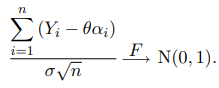
Последнее соотношение предоставляет возможность построить доверительный интервал для параметра θ; необходимо лишь заменить σ ее статистической оценкой. Согласно определению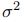 
получаем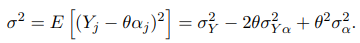 
Оценки теоретических характеристик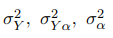 
в правой части имеют соответствующий
вид:
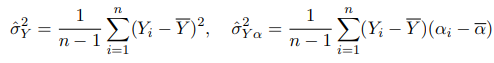
и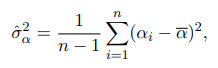 
и в результате состоятельной оценкой параметра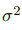 
является статистика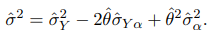 
Следовательно, доверительный интервал для параметра θ с уровнем значимости 2γ записывается в
виде:
где ˆθ = Y / α; z1−γ — квантиль уровня γ стандартного нормального распределения;
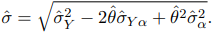
Так как при построении доверительного интервала используется параметр n — число циклов регенерации, то время моделирования N заранее не фиксируется. Ясно, что n ≈ N / α, и так
как величина α также не известна, то для оценивания ее и, следовательно, для оценивания времени моделирования N, можно провести несколько пробных этапов моделирования. Если же при
проведении имитационных экспериментов существуют ограничения на затраты машинного времени
и в процессе моделирования мы последовательно отслеживаем периоды и циклы регенерации, т.е.
n заранее не зафиксировано, то возникает необходимость с ростом n получать последовательность
оценок для интересующих нас параметров. Это осуществляется по следующим формулам (аргумент
n указывает на тот факт, что оценка получена на основе наблюдений за n циклами регенерации):
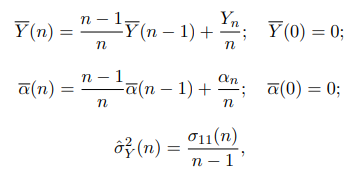
где
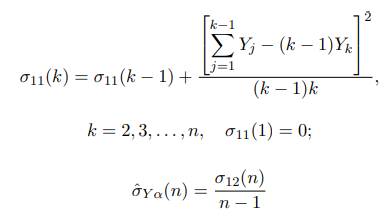
где
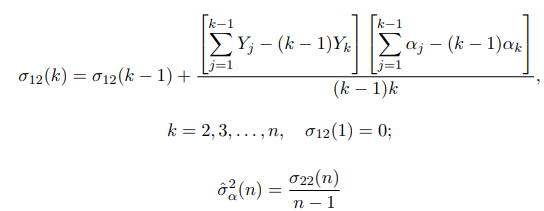
где
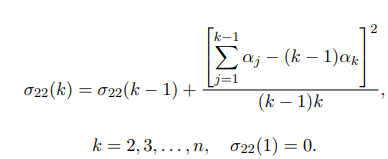
Кроме того можно отметить, что если имеется возможность выбора из более чем одной последовательности точек регенерации, то длины соответствующих доверительных интервалов будут
приблизительно равными при большом времени моделирования N. Отсюда следует, что можно выбирать любую наиболее удобную последовательность точек регенерации.
Но при выборе этих точек необходимо проявлять определенную осторожность. Дело в том, что
можно попасть в ситуацию, когда средняя длина периода регенерации бесконечна, или эта средняя
длина конечна, но достаточно велика, чтобы при имеющихся возможностях на затраты машинного
времени промоделировать необходимое число циклов регенерации.
Предположим, например, что моделируется однолинейная стационарная СМО с целью определения среднего времени ожидания. Пусть ωn — время ожидания n–го требования. Точками регенерации в рассматриваемом случае являются моменты возвращения процесса {ωn, n ≥ 1} в
какое–то фиксированное состояние, представляющее собой точку на неотрицательной половине
числовой оси. Если это состояние нулевое, то средняя длина периода регенерации конечна. Если
же это состояние зафиксировано ненулевым, то средняя длина периода регенерации бесконечна и
изложенная ранее методика получения доверительного интервала для W не применима.
В общем случае выход из возникшей ситуации состоит в том, чтобы в качестве моментов регенерации выбрать некоторое множество S, состоящее более чем из одной точки. Это множество
должно быть таким, чтобы среднее время возвращения в S было конечно и не велико до такой степени, чтобы в процессе моделирования получилось достаточное число циклов регенерации. Затем
в предположении, что процесс регенерируется каждый раз при попадании в S следует применить
ранее изложенную методику по расчету точечных оценок и доверительных интервалов для исследуемых параметров.
Описанная модификация носит название метода приближенной регенерации. Недостаток
этого метода заключается в отсутствии количественного расчета предположения о приближенной
регенерации на точность доверительного интервала, достоинство — в простоте численной реализации.
Для
Для регенеративного случайного процесса точечная оценка параметра и соответствующий доверительный интервал описывались выше. Укажем другие точечные оценки для и соответствующие доверительные интервалы.
Оценка Биля:
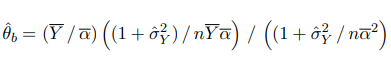
с доверительным интервалом:
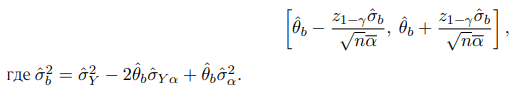
Оценка Филлера:
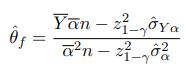
с доверительным интервалом:
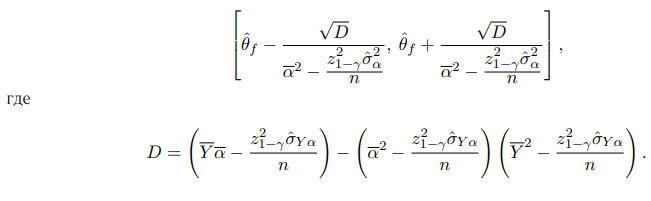
Оценка Тина:
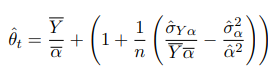
с доверительным интервалом
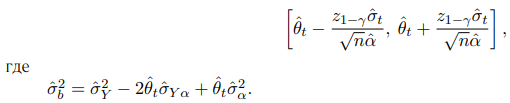
Оценка ”складного ножа”:
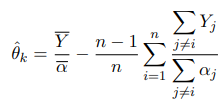
с доверительным интервалом
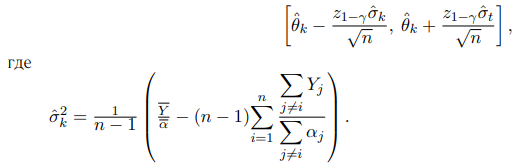
Приведенные оценки являются сильно состоятельными и более предпочтительными по сравнению с приведенной выше оценкой
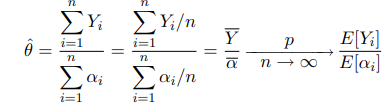, так как имеют меньшее смещение. Для малых выборок наименьшее смещение
и более точный доверительный интервал для θ дает оценка ”складного ножа”. Эта оценка
наиболее предпочтительна для малых значений n. При больших выборках все приведенные оценки
дают примерно одинаковые результаты.Для иллюстрации изложенных методов, изложенных, приведем алгоритмы моделирования конкретных СМО и укажем точечные оценки некоторых характеристик этих систем . Иногда точечные оценки параметров приводятся в виде отношения средних
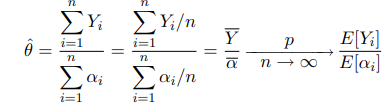. Для определения доверительных интервалов надо определить соответствующие регенерирующие процессы и обрабатывать получаемые экспериментальные данные регенеративным методом. Для выяснения вопроса о том, является ли конкретный случайный процесс регенерирующим, можно учитывать, например, тот факт, что регенерирующими процессами являются неприводимые и возвратные (с непрерывным или дискретным временем) цепи Маркова и полумарковские процессы с конечным или счетным пространством состояний.
Цель лабораторной работы заключается в реализации на вычислительном устройстве процесса функционирования СМО методами имитационного моделирования и проведении статистического анализа по оцениванию параметров СМО регенеративным методом. Выше приведен алгоритм, описывающий функционирование СМО. Это делается для обработки и методики моделирования, и способа обработки получающихся экспериментальных данных регенеративным методом. Параметры, характеризующие работу СМО (интенсивности входящего потока и обслуживания, число приборов и т. д.) следует выбирать такими, чтобы у рассматриваемых систем существовал стационарный режим. Число циклов регенерации n необходимо взять таким, чтобы выборочные оценки параметров отличались от теоретических значений этих параметров не более чем на заранее заданную величину