Семинар 1
1. Под высказыванием будем понимать такое предложение, про которое можно сказать, что оно истинно или ложно. Например, предложение „Хорошая ли сегодня погода? " не является высказыванием.
Определение „Треугольник называется равнобедренным, если две его стороны равны между собой" не является высказыванием.
Предложение „Если две стороны треугольника равны, то этот треугольник называется равнобедренным" является высказыванием.
2. Составное высказывание вида „А или В", где А и В — высказывания, считается ложным в тех случаях, когда оба высказывания А и В ложны. Во всех остальных случаях высказывание „А или В" истинно. Высказывание „2 > 3 или 5 — четное число" следует считать ложным, а высказывания „2 < 3 или 5 — четное число", „2 < 3 или 4 — четное число" — истинными.
3. Составное высказывание вида „А и В", где А и В — высказывания, считать истинным в тех случаях, когда оба высказывания А и В истинны. Во всех остальных случаях будем считать высказывание „А и В" ложным. Высказывание „2 < 3 и 4 — четное число" истинно, а высказывания: „2<3 и 5—четное число", „2>3 и 5 — четное число" — ложны.
Составное высказывание вида „Если А, то В", где А и В — высказывания, ложно в тех случаях, когда высказывание А истинно, а высказывание В ложно. Таким образом, высказывание „Если А, то В" с ложным А и любым В истинно. Высказывание „Если три стороны треугольника равны, то он является равносторонним" является истинным. Высказывание „Если 3 + 4 = 8, то 3 + 3 = 6" является истинным.
4. Из двух высказываний А и В можно составить теорему:
Если А, то В (1).
Здесь высказывание А называется условием, или посылкой, высказывание В — заключением.
Если В, то А, (2) - теорема обратная (1). (1) - теорема обратная (2). Теоремы (1) и (2) называются взаимно обратными.
5. Переменная, в область значений которой входят только истинностные значения: и , л, называется высказывательной переменной.
Операции над высказываниями
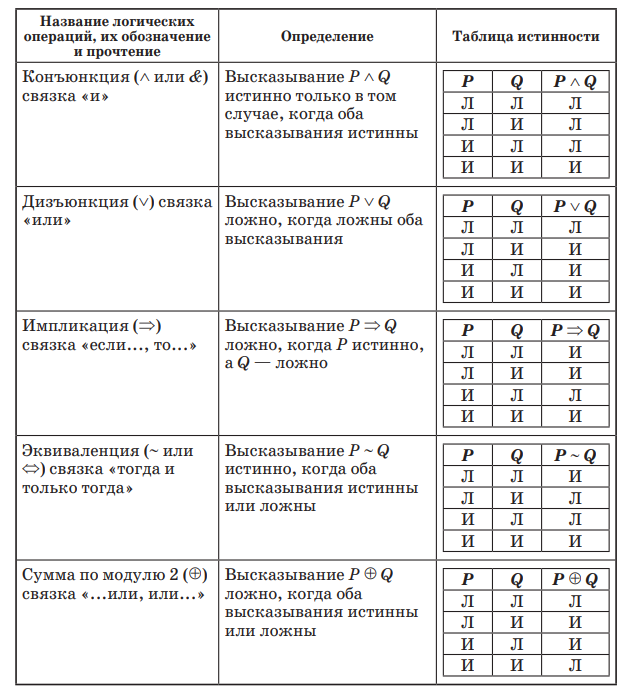
5.1. Отрицание высказывания А обозначается ~А и означает высказывание, имеющее истинностное значение, противоположное к истинностному значению высказывания А.
5.2. Дизъюнкция высказываний А и В обозначается А В и означает высказывание, истинное в том и только в том случае, когда истинно хотя бы одно из высказываний А и В. Дизъюнкции соответствует логическому союзу „или".
5.3. Конъюнкция высказываний А к В обозначается А & В и означает высказывание, истинное в том и только в том случае, когда истинно каждое из высказываний А и В.
5.4. Импликация высказываний А и В обозначается А В и означает высказывание, ложное в том и только в том случае, когда посылка А истинна и заключение В ложно. Операция импликации соответствует логическому союзу „если..., то".
5.5.Эквиваленция высказываний А и В обозначается А В и означает высказывание, истинное в том и только в том случае, когда высказывания А и В имеют одинаковое истинностное значение. Эквиваленция А В высказываний А и В означает то же, что высказывания „A тогда и только тогда, когда В", „Для того, чтобы А, необходимо и достаточно, чтобы В".
Формулы логики высказываний
Пропозициональные переменные— переменные, вместо которых можно подставлять конкретные высказывания. формула алгебры высказываний определяется по следующим правилам:
1) всякая пропозициональная переменная есть формула;
2) если F1 и F2 — формулы, то выражения ¬F, (F1 ∧ F2), (F1 ∨ F2), (F1 → F2), (F1 ⇔ F2) также являются формулами;
3) других формул, кроме построенных по правилам двух
предыдущих пунктов, нет.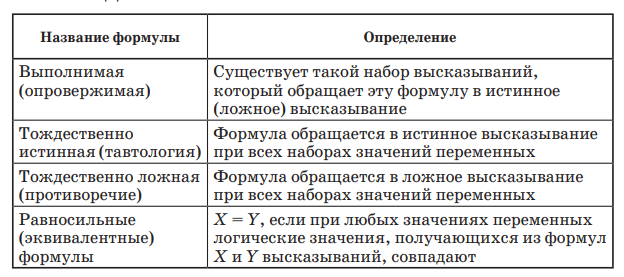
Пример выполнимой формулы (в последнем столбце таблицы)
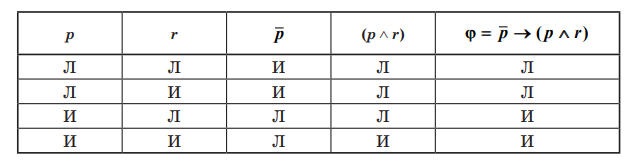
Пример формылы-тавтологии
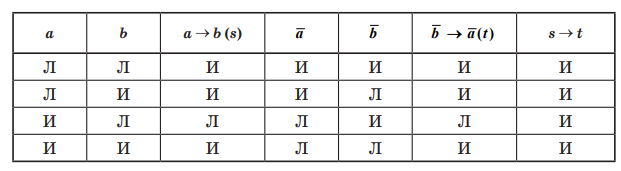
Примеры формул, связанных с импликацией
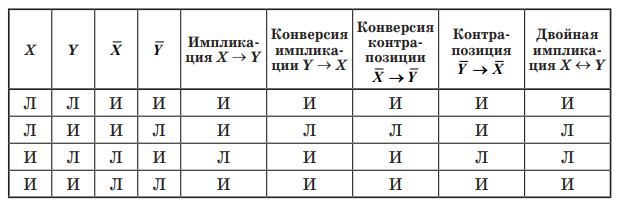
1. Х является достаточным условием для Y: если имеет место Х, то Y также будет иметь место. Импликация Х → Y.
2. Х является необходимым условием для Y: если имеет место Y, то Х также будет иметь место. Конверсия достаточного условия Y → X.
3. Х является необходимым и достаточным условием
для Y: Х имеет место, если и только если имеет место Y.
Двойная импликация (эквивалентность) X ∼ Y.
Пусть E = {H1, H2, ..., Hm} — конечное множество формул и A — формула. формула A называется логическим
следствием формул множества E, если A истинна на всякой интерпретации, на которой истинны одновременно
все формулы H1, ..., Hm. В этом случае используют запись
H1, ..., Hm |= A, котораяназывается правилом вывода, или
клаузой. формулы H1, ..., Hm называются гипотезами, или
посылками, или допущениями. формулу A называют заключением. Клауза верна, если формула A действительно
логическое следствие формул H1, ..., Hm, и неверна, если
логическое следствие места не имеет.
если вместо аргументов формул H1, ..., Hm, A подставить
конкретные высказывания, клауза наполнится конкретным содержанием, которое мы будем называть легендой.
Пусть имеет место клауза: H1, ..., Hm |=A.
1. Доказательство клаузы с помощью анализа таблицы истинности. Необходимо убедиться, что на всех наборах значений переменных, на которых гипотезы Н1, ..., Hn истинны одновременно, также равна 1 (И) формула А, которая проверяется на логическое следствие.
2. Доказательство от противного. Полагают, что заключение равно 0 (Л), и доказывают, что в этом случае
хотя бы одна из гипотез (посылок) обязательно равна 0 (Л).
Тогда логическое следствие имеет место. В противном случае (все гипотезы равны 1, а заключение равно 0) клауза
неверна.
Функцией алгебры логики (логической функцией, булевой функцией) n переменных называется функция
f(x1, ..., xn), принимающая значения 0 или 1, аргументы
которой также принимают значения 0 или 1. Константу 1
по-другому называют истиной, а константу 0 — ложью.
Аргументы логической функции называют логическими (булевыми) переменными.
Для одной переменной:

Для двух переменных:
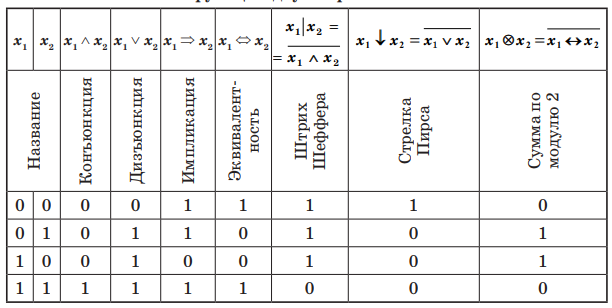
Иерархия операций (в порядке убывания старшинства)
задается так: (&, |, ↓), ∨, →, (∼, ⊕). В скобках указаны равносильные операции.
Выполнить следующие задания:
1. Выберите несколько вариантов ответа.
Высказываниями являются...
Варианты ответа: 1) 2 + 2 – 4; 2) тюльпаны бывают
красные; 3) привет, ученик! 4) 2 + 2 = 5.
2. Выберите один вариант ответа. Сложным называется высказывание, полученное из простых с помощью грамматических связок:
Варианты ответа: 1) «только тогда... когда», «если..., то...»; 2) «не», «и», «или», «тогда и только тогда...», «если.., то...»;
3) «не», «и», «или»; 4) «не», «тогда и только тогда...», «если..., то...».
3. Выберите один вариант ответа. Логическому высказыванию «Точка x принадлежит интервалу (a, b)» соответствует логическое выражение...
Варианты ответа: 1) (x < a) или (x > b); 2) (x > a) и (x < b); 3) не (x < a) или (x < b); 4) (x > a) или (x > b).
4. Выберите один вариант ответа. Логическое значение высказывания A ∨ ⋅ ( ) 2 2 = 4 , если высказывание А ложно, есть...
Варианты ответа: 1) истина; 2) ложь; 3) правда; 4) неправда.
5. Выберите один вариант ответа. Значение логического выражения (1 ∨ 1) ∧ (1 ∨ 0) равно...
Варианты ответа: 1) 1; 2) 0; 3) 10; 4) 2
6. Выберите ответы согласно тексту задания. Установите соответствие между высказываниями и соответствующими им логическими формулами:
1) число 7 нечетное (A) и двузначное (B); 2) если число четное (A), то оно делится на 2 (B);
3) водительские права можно получить (A) тогда и только тогда, когда тебе исполнится 18 (B);
4) неверно, что корова — хищное животное (A). a) А → В; b) А ∧ В; c) А ⇔ В; d) ¬А; e) А ∨ В.
7. Выберите один вариант ответа. Укажите составное высказывание, построенное из высказываний А, В, и С, которое истинно тогда и только тогда, когда все данные высказывания истинны. Варианты ответа: 1) А ∧ В ∧ С; 2) (А ∧ В) → С; 3) А ∨ В ∨ С; 4) (А ∨ В) → С
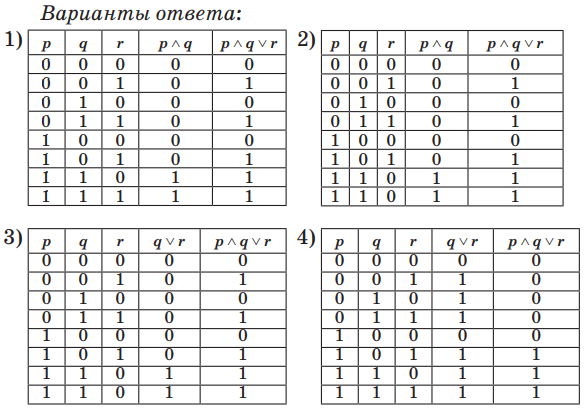
8. Выберите один вариант ответа. Укажите правильную таблицу истинности высказывания p ∧ q ∨ r... Варианты ответа:
9. Выберите один вариант ответа. Необходимым и достаточным условием делимости натурального числа N на 60 является его делимость...
Варианты ответа: 1) на 2, на 10 и на 3; 2) на 6 и на 10; 3) на 3, на 4 и на 5; 4) на 2 и на 30.
10. Выберите несколько вариантов ответа. Обозначим утверждение «четырехугольник является ромбом» через А, утверждение «диагонали четырехугольника перпендикулярны» через В. Тогда в теореме «диагонали ромба перпендикулярны» условие... Варианты ответа: 1) А достаточно для В; 2) В необходимо для А; 3) В достаточно для А; 4) А необходимо для В.
11. . Выберите один вариант ответа. Необходимым и достаточным условием делимости натурального числа N на 60 является его делимость...
Варианты ответа: 1) на 2, на 10 и на 3; 2) на 6 и на 10; 3) на 3, на 4 и на 5; 4) на 2 и на 30.
12. Выберите один вариант ответа. Булевой функции f(x1, x2): f(1, 0) = 1 соответствует формула...
Варианты ответа: 1) x1 → x2; 2) x1 ∨ x2; 3) x1 ∧ x2; 4) x1 ⇔ x2.
13. Выберите один вариант ответа. Значение логического выражения (1 → 1) ∧ (1 ∨ 0) равно...
Варианты ответа: 1) 1; 2) 0; 3) 10; 4) 2.
14. Выберите один вариант ответа. формула X → (Y ∧ Z) эквивалента формуле...
Варианты ответа: 1)X ∧ (Y → Z); 2)(X → Y) ∧ (X → Z); 3) (X → Y) ∨ (X → Z); 4) Y ∧ (X → Z).
15. Выберите один вариант ответа. формула (X → Y) ∨ Z эквивалентна формуле...
Варианты ответа: 1) X ∨ (Y → Z); 2) (X → Y) ∨ (X → Z); 3) (X → Y) ∨ (Y → Z); 4) (X ∨ Z) → (Y ∨ Z).