Методические указания к лр 1
I. Оценка корреляции зависимой и независимой переменных
#Оценка корреляции зависимой и независимой переменной на dataset House Sale Price Dataset.csv
Data_HousePrice <-read.csv("Dataset/House Sale Price Dataset.csv",header=TRUE);
#Построение векторов Y-зависимая, X-независимая
y <-Data_HousePrice$HousePrice;
x<-Data_HousePrice$StoreArea;
#Построение Scatter Plot
plot(x,y, main="Scatterplot HousePrice vs StoreArea", xlab="StoreArea(sqft)", ylab="HousePrice($)", pch=19,cex=0.3,col="red")
#Добавление линии подгонки для демонстрации тренда отношения
abline(lm(y~x)) # regression line (y~x)
#построение модели линейной регрессии - функция lm
lines(lowess(x,y), col="green") # lowess line (x,y)
cat("The correlation among HousePrice and StoreArea is ",cor(x,y));
The correlation among HousePrice and StoreArea is 0.62.
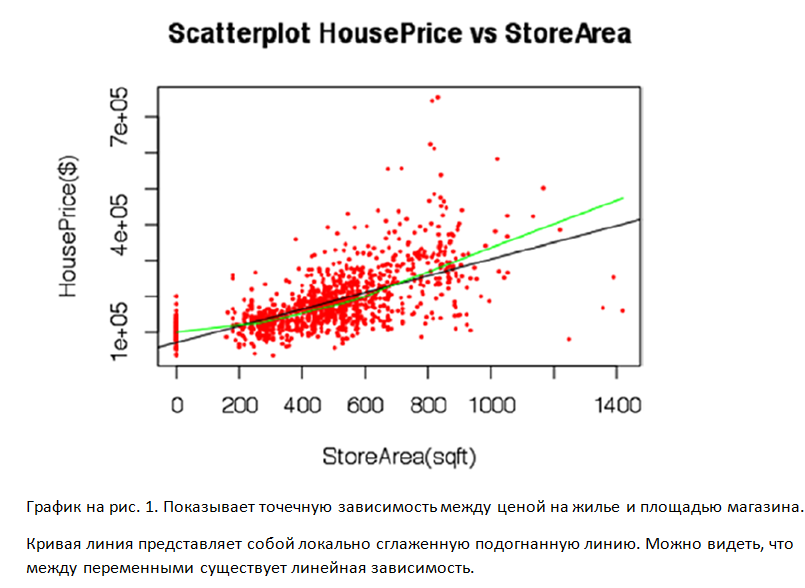
Выводы по визуализации:
1.
Корреляция имеет положительное направление, поэтому в среднем
цена дома увеличивается с размером магазина. Следовательно, чем больше места
магазина, тем лучше дом, что означает, что он дороже.
2. Корреляция составляет 0,62. Это умеренно прочные отношения.
3. Изогнутая линия - это LOWESS (Locally Weighted Scatterplot Smoothing). График показывает, что характер визуализации близок к линейной регрессии. Следовательно, линейные отношения мождно принять для этой модели.
4. На визуализации присутствует вертикальная линия для Storearea = 0. Что говорит о том, что цены варьируются для дома, где нет зоны магазина. Нужно найти другие факторы, которые влияют на цену на дом.
Линейная регрессия
Линейная регрессия - это процесс подбора линейной функции-предиктора для оценки неизвестных параметров на основе исходных данных. В общем случае модель предсказывает условное среднее значение Y при заданном X, которое является аффинной функцией от X.
Модель линейной регрессии позволяет выполнить:
• прогнозирование
• количественную оценку взаимосвязи между переменными (например, параметры и p-значения)
Математически, простая линейная зависимость выглядит следующим образом:
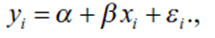
где y - прогнозируемый отклик (или установленное значение) a - промежуточное значение, т.е. среднее значение отклика, если независимая переменная равна нулю, а β - параметр для x, т.е. изменение y на единицу изменения x.
Далее, в качестве функции потерь будем использовать метод наименьших квадратов (OLS).
В OLS алгоритм минимизирует ошибку квадратов. Задачу минимизации можно сформулировать следующим образом:
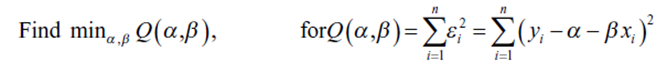
Поскольку это параметрический метод, мы можем получить решение в замкнутой форме для этой
оптимизации. Решение в замкнутой форме для оценки коэффициентов (или параметров) заключается в использовании следующих уравнений:
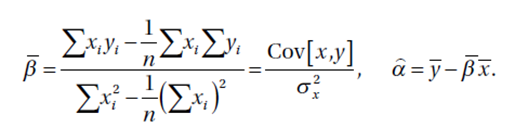
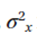-дисперсия х
Существует теорема Гаусса- Теорема Маркова, которая гласит, что при выполнении следующих условий:
• Математическое ожидание (среднее значение) остатков равно нулю (нормальность остатков).
• Остатки не коррелируют и (автокорреляция отсутствует)
• Остатки имеют одинаковую дисперсию (гомоскедастичность - свойство, означающее постоянство условной дисперсии вектора или последовательности случайных величин.)
тогда обычная оценка методом наименьших квадратов дает наилучшую линейную несмещенную оценку коэффициентов (или оценок параметров). Существуют ключевые понятия, которые составляют наилучшую оценку:
- искажение (bias) — это разница между ожиданием оцениваемой величины и ее значением;,
- согласованность (consistent). В области статистики термин “согласованный” относится к свойству оценщика, при котором по мере увеличения размера выборки оценки с вероятностью приближаются к истинному значению параметра. Эта концепция имеет решающее значение для обеспечения того, чтобы статистические методы давали надежные результаты по мере сбора большего количества данных. Согласованная оценка обеспечивает основу для составления выводов о совокупности на основе выборочных данных
- эффективность. Эффекти́вная оце́нка в математической статистике — наилучшая оценка в среднеквадратичном смысле.
Простая линейная регрессия (функция lm() в R)
Теперь мы можем перейти к оценке линейных моделей с использованием метода OLS. lm() - функция из пакета на языке R, предоставляет возможность запускать OLS для линейных регрессий. lm() может использоваться для проведения регрессионного анализа, одноуровневого дисперсионного анализа и анализа ковариации. Она является частью пакета base stats() в R.
II. Построение модели линейной регрессии в R
Построим простую линейную регрессию чтобы понять, как интерпретировать
выходные данные lm() для этого простого случая. Здесь мы применяем модель линейной регрессии с использованием метода OLS к:
- Зависимой переменной: Цена дома (HousePrice)
- Независимой переменной: Площадь магазина (x - StoreArea).
Корреляционный анализ показал, что эти две переменные имеют положительную
линейную связь, и, следовательно, можно ожидать положительного знака для оценочных параметров StoreAra.
# построение модели
fitted_Model <-lm(y~x)
# вывод статистики по модели
summary(fitted_Model)
Call:
lm(formula = y ~ x)
Residuals:
Min 1Q Median 3Q Max
-280115 -33717 -4689 24611 490698
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 70677.227 4261.027 16.59 <2e-16 ***
x 232.723 8.147 28.57 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 63490 on 1298 degrees of freedom
Multiple R-squared: 0.386, Adjusted R-squared: 0.3855
F-statistic: 816 on 1 and 1298 DF, p-value: < 2.2e-16
Получаем уравнение
модели:
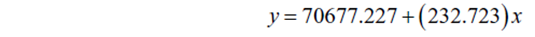
y - HousePrice
x - StoreArea.
Значение 232.723 говорит о том, что на каждую единицу StoreАrea, HomeРrice увеличивается на 232,72 долл. США.
Значение 70677.227, при отсутствии StoreArea означает, что 70677.227 можно рассматривать, как первоначальный взнос.
Рассмотрим статистику lm (), чтобы лучше понять модель.
- Call: Выводит уравнение модели, полученное функцией lm
- Residuals(остатки): Выводит диапазон остатков, Min, Max, медиану остатков. Отрицательная медиана означает, что по крайней мере половина остатков отрицательна, т.е. прогнозируемые значения превышают фактические более чем на 50%.
- Coefficients (коэффициенты): Это таблица, в которой приведены оценки параметров модели (или коэффициенты), стандартная ошибка, t-значение и p-значение t-критерия Стьюдента.
- Diagnostics (Диагностика): остаточная стандартная ошибка, а также множественные и скорректированные R-квадрат и F-статистика для тестирования дисперсии.
После оценки модели в целом и значимость каждого предиктора, мы перейдем к рассмотрению того, насколько модель соответствует фактическим значениям. Это делается путем сопоставления фактических значений с прогнозируемыми:
res<-stack(data.frame(Observed = y, Predicted =fitted(fitted_Model)))
res <-cbind(res, x =rep(x, 2))
#график строится через библиотеку lattice, xyplot(function)
install.packages("lattice")
library("lattice")
xyplot(values ~x, data = res, group = ind, auto.key =TRUE)
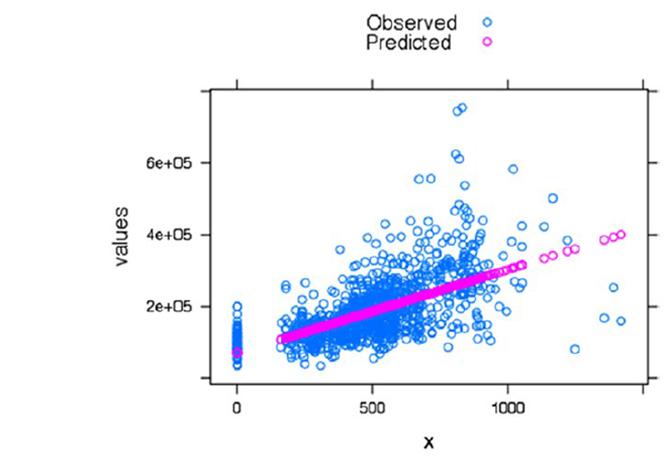
Визуализация показывает, что тренды прогнозируемых и фактических значений совпадают.
В этой модели использовалась только одна независимая переменная (площадь магазина), но доступны и другие переменные, которые показывают значительную взаимосвязь с ценами на жилье. Можно добавлять в регрессионный анализ несколько независимых переменных. - множественная линейная регрессия
III. Построение модели мультилинейной регрессии в R
Идеи простой линейной регрессии могут быть распространены на множество независимых переменных.
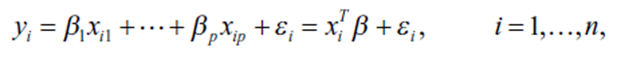
Для множественной регрессии очень популярно матричное представление, поскольку оно упрощает объяснение концепций матричных вычислений. Тогда линейная зависимость при множественной линейной регрессии становится
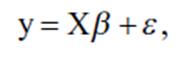
Ранее использовалась только одна переменная для объяснения зависимой переменной -StoreAria. В множественной линейной регрессии мы будем использовать StoreArea, StreetHouseFront, BasementArea, LawnArea, Rating, and SaleType в качестве независимых переменных для оценки линейной зависимости от HousePrice.
Функция оценки методом наименьших квадратов остается прежней, за исключением того, что в качестве предикторов будут использоваться новые переменные.
Чтобы выполнить анализ по нескольким переменным, мы вводим еще один шаг очистки данных - идентификацию пропущенного значения. Можно либо ввести пропущенное значение указав конкретное или не учитывать его в анализе. Если не учитывать, то используем функцию na.omit(). Следующий код сначала находит пропущенные случаи, а затем удаляет их.
# использование lm для создания мультилинейной регрессии
Data_lm_Model <-Data_HousePrice[,c("HOUSE_ID","HousePrice","StoreArea","Str
eetHouseFront","BasementArea","LawnArea","Rating","SaleType")];
# below function we display number of missing values in each of the variables in data
sapply(Data_lm_Model, function(x) sum(is.na(x)))
HOUSE_ID HousePrice StoreArea StreetHouseFront
0 0 0 231
BasementArea LawnArea Rating SaleType
0 0 0 0
# 231 случай ошибочных значений в StreetHouseFront. Функция Na.omit исправит их.
Data_lm_Model <-na.omit(Data_lm_Model)
rownames(Data_lm_Model) <-NULL
#категориальные переменные должны стать факторами
Data_lm_Model$Rating <-factor(Data_lm_Model$Rating)
Data_lm_Model$SaleType <-factor(Data_lm_Model$SaleType)
fitted_Model_multiple <-lm(HousePrice ~StoreArea +StreetHouseFront
+BasementArea +LawnArea +Rating +SaleType,data=Data_lm_Model)
summary(fitted_Model_multiple)
Call:
lm(formula = HousePrice ~ StoreArea + StreetHouseFront + BasementArea +
LawnArea + Rating + SaleType, data = Data_lm_Model)
Residuals:
Min 1Q Median 3Q Max
-485976 -19682 -2244 15690 321737
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.507e+04 4.827e+04 0.519 0.60352
StoreArea 5.462e+01 7.550e+00 7.234 9.06e-13 ***
StreetHouseFront 1.353e+02 6.042e+01 2.240 0.02529 *
BasementArea 2.145e+01 3.004e+00 7.140 1.74e-12 ***
LawnArea 1.026e+00 1.721e-01 5.963 3.39e-09 ***
Rating2 -8.385e+02 4.816e+04 -0.017 0.98611
Rating3 2.495e+04 4.302e+04 0.580 0.56198
Rating4 3.948e+04 4.197e+04 0.940 0.34718
Rating5 5.576e+04 4.183e+04 1.333 0.18286
Rating6 7.911e+04 4.186e+04 1.890 0.05905 .
Rating7 1.187e+05 4.193e+04 2.830 0.00474 **
Rating8 1.750e+05 4.214e+04 4.153 3.54e-05 ***
Rating9 2.482e+05 4.261e+04 5.825 7.61e-09 ***
Rating10 2.930e+05 4.369e+04 6.708 3.23e-11 ***
SaleTypeFirstResale 2.146e+04 2.470e+04 0.869 0.38512
SaleTypeFourthResale 6.725e+03 2.791e+04 0.241 0.80964
SaleTypeNewHouse 2.329e+03 2.424e+04 0.096 0.92347
SaleTypeSecondResale -5.524e+03 2.465e+04 -0.224 0.82273
SaleTypeThirdResale -1.479e+04 2.613e+04 -0.566 0.57160
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 41660 on 1050 degrees of freedom
Multiple R-squared: 0.7644, Adjusted R-squared: 0.7604
F-statistic: 189.3 on 18 and 1050 DF, p-value: < 2.2e-16
Оценочная модель содержит шесть независимых переменных, из которых четыре непрерывные
("StoreArea","StreetHouseFront","BasementArea","LawnArea") и две категориальные переменные ("Rating","SaleType"). Из результатов функции lm() видно, что "StoreArea","StreetHouseFront","BasementArea","LawnArea" являются значимыми при уровне достоверности 95%, т.е. статистически отличающимися от нуля. В то время как все SaleType незначимы, статистически они равны нулю. Из модели следует исключить SaleType и провести переоценку, чтобы сохранить только значимые переменные.
Следует сравнить фактические и прогнозируемые значения для этой модели, построив их после упорядочения рядов по ценам на жилье.
#Get the fitted values and create a data frame of actual and predicted get predicted values
actual_predicted <-as.data.frame(cbind(as.numeric(Data_lm_Model$HOUSE_
ID),as.numeric(Data_lm_Model$HousePrice),as.numeric(fitted(fitted_Model_
multiple))))
names(actual_predicted) <-c("HOUSE_ID","Actual","Predicted")
#Ordered the house by increasing Actual house price
actual_predicted <-actual_predicted[order(actual_predicted$Actual),]
#Find the absolute residual and then take mean of that
install.packages("ggplot2")
library(ggplot2)
#Plot Actual vs Predicted values for Test Cases
ggplot(actual_predicted,aes(x =1:nrow(Data_lm_Model),color=Series)) +
geom_line(data = actual_predicted, aes(x =1:nrow(Data_lm_Model),
y = Actual, color ="Actual")) +
geom_line(data = actual_predicted, aes(x =1:nrow(Data_lm_Model),
y = Predicted, color ="Predicted")) +xlab('House Number') +ylab('House
Sale Price')
График на рисунке показывает фактические и прогнозируемые значения для упорядоченной стоимости. График также показывает линейную зависимость, предсказанную нашей моделью, в сочетании с точечной диаграммой оригинала.
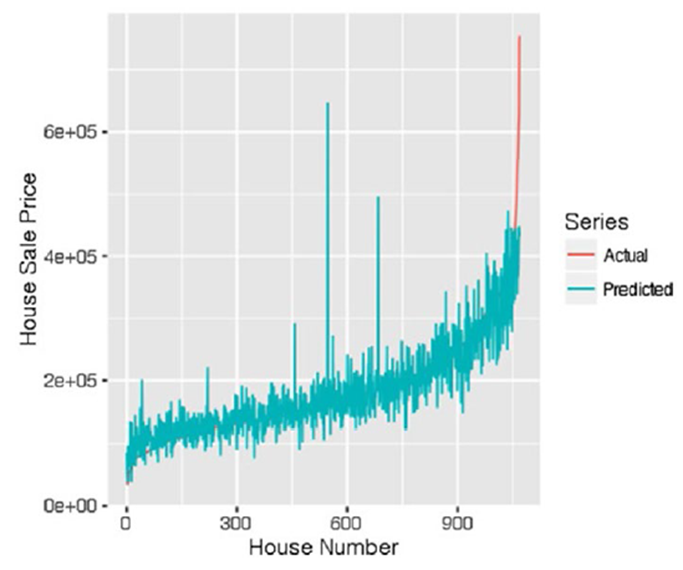
Цены на жилье расположены в порядке возрастания, чтобы увидеть меньший разброс между фактическими и прогнозируемыми ценами. График показывает, что наша модель точно соответствует фактическим ценам.
Есть несколько случаев повышенных значений, которые модель не в состоянии предсказать, и это нормально, поскольку на нашу модель не влияют выбросы.
IV. Диагностика модели
Диагностика модели является важным этапом в процессе выбора модели. Существует разница между оценкой производительности модели, рассмотренной ранее, и процессом выбора модели. При оценке модели мы проверяем, как модель работает на неизвестных данных (тестовых данных), но при выборе модели мы видим, как сама модель соответствует нашим данным. Это включает в себя проверку значимости p-значений оценок параметров, нормальности, автокорреляции, гомоскедастичности, точек влияния/выбросов и мультиколлинеарности. Существуют и другие тесты, позволяющие определить, насколько хорошо модель следует статистическим допускам, строгой экзогенности, таблицам дисперсии и т.д. В линейной регрессии экстремальные значения могут создавать проблемы в процессе оценки. Несколько больших значений вносят искажение в оценках и создают другие аберрации в остатках. Так что важно определить влиятельные точки в данных. Если влиятельные точки кажутся слишком экстремальными, мы должны отказаться от них в процессе анализа, как от выбросов. Рассмотрим конкретную статистическая меру-расстояние Кука.
Расстояние Кука
Этот метод используется для поиска влиятельных точек в данных. Расстояние Кука измеряет эффект удаления данного наблюдения.
Таким образом, если удаление какого-либо наблюдения приводит к значительным изменениям, это означает, что эти точки влияют на регрессионную модель. Этим точкам присваивается большое значение Расстояния Кука и они рассматриваются для дальнейшего изучения.
Граничное значение для этой статистики может быть принято как Di > 4 / n, где n - количество наблюдений. Если сделаеть поправку на количество параметров в модели, то предельное значение можно принять равным Di>4/ n-k-1, где k - количество переменных в модели.
install.packages("car")
library(car);
# график расстояний Кука
# identify D values > 4/(n-k-1)
cutoff <-4/((nrow(Data_lm_Model)-length(fitted_Model_
multiple$coefficients)-2))
plot(fitted_Model_multiple, which=4, cook.levels=cutoff)
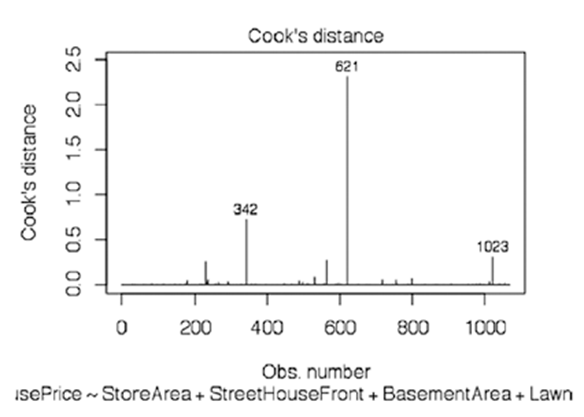
На графике на рис. выделены номера наблюдений с большим расстоянием Кука. Эти наблюдения требуют дальнейшего изучения.
# Influence Plot
influencePlot(fitted_Model_multiple, id.method="identify",
main="Influence Plot", sub="Circle size is proportional to Cook's
Distance",id.location =FALSE)
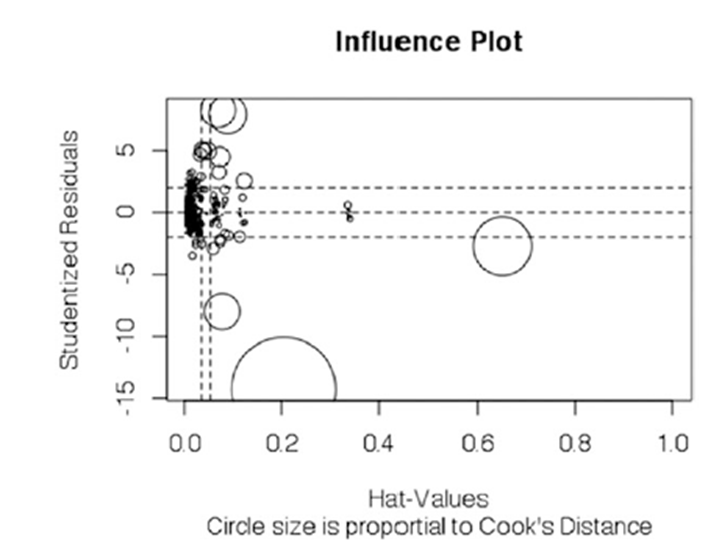
График на рис. 6-17 показывает другое представление расстояния Кука. Размер круга пропорционален этому расстоянию.
Кроме того, здесь показаны результаты теста на выбросы:
#обнаружение выбросов
outlier.test(fitted_Model_multiple)
rstudent unadjusted p-value Bonferonni p
621 -14.285067 1.9651e-42 2.0987e-39
229 8.259067 4.3857e-16 4.6839e-13
564 -7.985171 3.6674e-15 3.9168e-12
1023 7.902970 6.8545e-15 7.3206e-12
718 5.040489 5.4665e-07 5.8382e-04
799 4.925227 9.7837e-07 1.0449e-03
235 4.916172 1.0236e-06 1.0932e-03
487 4.673321 3.3491e-06 3.5768e-03
530 4.479709 8.2943e-06 8.8583e-03
Номера — 342,621 и 102, как показано на рисунке
(соответствуют номерам домов 412, 759 и 1242) - это три основные точки влияния.
Можно рассмотреть эти записи, чтобы посмотреть, какими значениями они обладают.
#Pull the records with highest leverage
Debug <-Data_lm_Model[c(342,621,1023),]
[1] " The observed values for three high leverage points"
Debug
HOUSE_ID HousePrice StoreArea StreetHouseFront BasementArea LawnArea
342 412 375000 513 150 1236 215245
621 759 160000 1418 313 5644 63887
1023 1242 745000 813 160 2096 15623
Rating SaleType
342 7 NewHouse
621 10 FirstResale
1023 10 SecondResale
print("Model fitted values for these high leverage points");
[1] "Model fitted values for these high leverage points"
fitted_Model_multiple$fitted.values[c(342,621,1023)]
342 621 1023
441743.2 645975.9 439634.3
print("Summary of Observed values");
[1] "Summary of Observed values"
summary(Debug)
HOUSE_ID HousePrice StoreArea StreetHouseFront
Min. : 412.0 Min. :160000 Min. : 513.0 Min. :150.0
1st Qu.: 585.5 1st Qu.:267500 1st Qu.: 663.0 1st Qu.:155.0
Median : 759.0 Median :375000 Median : 813.0 Median :160.0
Mean : 804.3 Mean :426667 Mean : 914.7 Mean :207.7
3rd Qu.:1000.5 3rd Qu.:560000 3rd Qu.:1115.5 3rd Qu.:236.5
Max. :1242.0 Max. :745000 Max. :1418.0 Max. :313.0
BasementArea LawnArea Rating SaleType
Min. :1236 Min. : 15623 10 :2 FifthResale :0
1st Qu.:1666 1st Qu.: 39755 7 :1 FirstResale :1
Median :2096 Median : 63887 1 :0 FourthResale:0
Mean :2992 Mean : 98252 2 :0 NewHouse :1
3rd Qu.:3870 3rd Qu.:139566 3 :0 SecondResale:1
Max. :5644 Max. :215245 4 :0 ThirdResale :0
(Other):0
Цены на жилье для этих трех точек влияния далеки от среднего значения или высокой плотности. Цена на жилье для двух наблюдений соответствует самой высокой и самой низкой в наборе данных. Также интересно то, что третье наблюдение, соответствующее средней цене дома, имеет очень большую площадь газона, что, безусловно, оказывает влияние. Основываясь на этом анализе, мы можем либо вернуться назад, чтобы проверить, являются ли эти данные ошибками, либо проигнорировать их в нашем анализе.
Проверка нормальности остатков (тесты)
Остатки являются основой для диагностики регрессионных моделей. Нормальность остатков является важным условием для того, чтобы модель была корректной моделью линейной регрессии. Нормальность подразумевает, что ошибки/остатки являются случайным шумом, и наша модель отражает всю информацию в данных. Модель линейной регрессии дает нам условные ожидания функции y для заданных значений х. Однако в подобранном уравнении есть некоторый остаток. Нам нужно, чтобы математическое ожидание остатка было нормально распределено со средним значением 0 или приводимым к 0. A нормальная остаточная величина означает, что вывод модели (доверительный интервал,значимость предикторов модели) верен. Распределение стьюдентизированных остатков (их можно рассматривать как нормализованное значение) -хороший способ определить, выполняется ли предположение о нормальности или нет. Формально проверить остатки можно с помощью тестов на нормальность, таких как тесты KS, тесты Шапиро-Уилка, Андерсона, Тесты Дарлинга и т.д.
Вывод графика на стьюдентизированных остатках для нормального распределения, которое образует кривую колокола.
install.packages("stats")
library(stats)
install.packages("IDPmisc")
library(IDPmisc)
Loading required package: grid
install.packages("MASS")
library(MASS)
sresid <-studres(fitted_Model_multiple)
#очистка некорректных значений (NAN/Inf/NAs)
sresid <-NaRV.omit(sresid)
hist(sresid, freq=FALSE,
main="Distribution of Studentized Residuals",breaks=25)
xfit<-seq(min(sresid),max(sresid),length=40)
yfit<-dnorm(xfit)
lines(xfit, yfit)
График на рис. создан с использованием детализированных остатков. В предыдущем коде остатки были детализированы с помощью функции studres() в R.
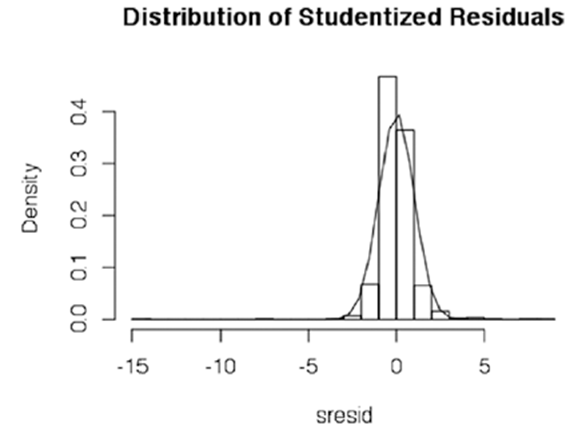
Рисунок. Распределение стьюдентизированных остатков
График остаточных значений близок к нормальному, поскольку распределение образует колоколообразную кривую.
Проведем формальную проверку на нормальность.
Тест Колмогорова-Смирнова (тест KS) и другие тесты
Статистика Колмогорова–Смирнова для данной кумулятивной функция распределения F(x) равна
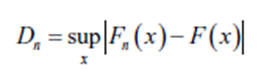
где sup x - максимальное значение из набора расстояний.
Статистика KS показывает наибольшую разницу между эмпирическим распределением
остаточных значений и нормальным распределением. Если наибольшее значение (supremum) превышает критическое значение, то распределение не является нормальным (используя p-значение тестовой статистики). Ниже приведены три теста на соответствие результатов:
# test on normality
#1. KS one sample test
ks.test(fitted_Model_multiple$residuals,pnorm,alternative="two.sided")
One-sample Kolmogorov-Smirnov test
data: fitted_Model_multiple$residuals
D = 0.54443, p-value < 2.2e-16
alternative hypothesis: two-sided
#2. Shapiro Wilk Test
shapiro.test(fitted_Model_multiple$residuals)
Shapiro-Wilk normality test
data: fitted_Model_multiple$residuals
W = 0.80444, p-value < 2.2e-16
#3. ADarling-Darling Test
install.packages("nortest")
library(nortest)
ad.test(fitted_Model_multiple$residuals)
Anderson-Darling normality test
data: fitted_Model_multiple$residuals
A = 29.325, p-value < 2.2e-16
Ни один из этих трех тестов не предполагает, что остатки распределены нормально. Значения p меньше 0,05, и, следовательно, мы можем отклонить нулевую гипотезу о
нормальном распределении. Это означает, что мы должны вернуться к нашей модели и посмотреть, что может быть причиной необычного поведения, исключить какую-то переменную или добавить какую-то переменную, важные моменты и другие проблемы.
Мультиколлинеарность
Мультиколлиниарность в основном является проблемой слишком большой информации в паре независимых переменных. Это явление, когда две или более переменных сильно коррелированы, и, следовательно, вызывают увеличение стандартные ошибки в модели. Для тестирования этого явления можно использовать корреляционную матрицу и посмотреть, имеются ли отношения с достойной точностью. Если да, добавление одной переменной достаточно для подачи информации, необходимой для объяснения зависимой переменной. В этом разделе мы будем использовать коэффициент увеличения дисперсии для определения степени многопрофильности независимых переменных. Еще одним популярным методом определения мультиколлинеарности является индекс Колина (Condition Index).
Коэффициент увеличения дисперсии (VIF) для мультиколлинеарности определяется следующим образом:
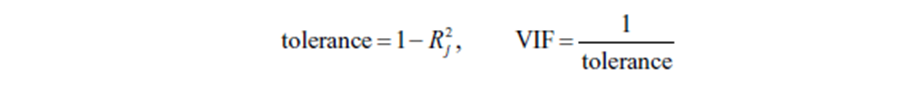
где R2 - коэффициент детерминации регрессии экспланатора (переменная, которая предсказывает или объясняет изменение другой переменной; объясняющая переменная.) j объясняющей все
остальные экспланаторы. Как правило, пороговыми значениями для определения наличия мультиколлинеарности на основе показателей являются:
• Допуск менее 0,20
• Значение VIF, равное 5 и более, указывает на проблему мультиколлинеарности
Простым решением этой проблемы является исключение переменной из этих пороговых значений в процессе построения модели.
library(car)
# calculate the vif factor
# Evaluate Collinearity
print(" Variance inflation factors are ");
[1] " Variance inflation factors are "
vif(fitted_Model_multiple);
# variance inflation factors
GVIF Df GVIF^(1/(2*Df))
StoreArea 1.767064 1 1.329309
StreetHouseFront 1.359812 1 1.166110
BasementArea 1.245537 1 1.116036
LawnArea 1.254520 1 1.120054
Rating 1.931826 9 1.037259
SaleType 1.259122 5 1.023309
print("Tolerance factors are ");
[1] "Tolerance factors are "
1/vif(fitted_Model_multiple)
GVIF Df GVIF^(1/(2*Df))
StoreArea 0.5659106 1.0000000 0.7522703
StreetHouseFront 0.7353955 1.0000000 0.8575521
BasementArea 0.8028664 1.0000000 0.8960281
LawnArea 0.7971175 1.0000000 0.8928143
Rating 0.5176450 0.1111111 0.9640796
SaleType 0.7942043 0.2000000 0.9772220
Теперь есть значения VIF и допуска, указанные в предыдущих таблицах. Применим ограничения для VIF и допуска.
# Apply the cut-off to VIF
print("Apply the cut-off of 4 for vif")
[1] "Apply the cut-off of 4 for vif"
vif(fitted_Model_multiple) >4
GVIF Df GVIF^(1/(2*Df))
StoreArea FALSE FALSE FALSE
StreetHouseFront FALSE FALSE FALSE
BasementArea FALSE FALSE FALSE
LawnArea FALSE FALSE FALSE
Rating FALSE TRUE FALSE
SaleType FALSE TRUE FALSE
# Apply the cut-off to Tolerance
print("Apply the cut-off of 0.2 for vif")
[1] "Apply the cut-off of 0.2 for vif"
(1/vif(fitted_Model_multiple)) <0.2
GVIF Df GVIF^(1/(2*Df))
StoreArea FALSE FALSE FALSE
StreetHouseFront FALSE FALSE FALSE
BasementArea FALSE FALSE FALSE
LawnArea FALSE FALSE FALSE
Rating FALSE TRUE FALSE
SaleType FALSE FALSE FALSE
Столбец GVIF имеет значение false для значений, которые установлены для мультиколлинеарности. Следовательно, можно с уверенностью сказать, что в модели нет проблемы мультиколлинеарности. И, следовательно, стандартные ошибки не завышены, так что можно провести проверку гипотез.
Автокорреляция остатков
Корреляция определяется между двумя различными переменными, в то время как автокорреляция, также известная, как последовательная корреляция, представляет собой корреляцию переменной самой с собой в разные моменты времени или в ряде. Этот тип взаимосвязи очень важен и довольно часто используется при моделировании временных рядов. Автокорреляция имеет больше смысла, когда есть определенный порядок в наблюдениях, например, индекс по времени, ключу и т.д. Если остаток показывает, что он имеет
определенную связь с предыдущими остатками, т.е. автокоррелирован, то шум возникает не случайно, а это означает, что все еще есть дополнительная информация, которую можно извлечь и ввести в модель. Для проверки автокорреляции используем самый популярный метод -
тест Дурбина Уотсона. Учитывая, что в процессе были определены среднее значение и дисперсия, статистика автокорреляции теста Дурбина Уотсона может быть определена следующим образом:
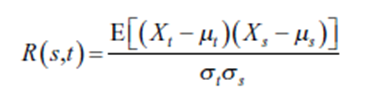
Это может быть переписано для нашей остаточной автокорреляции как статистика теста d-Durbin Watson:
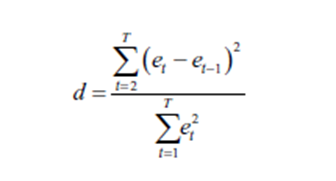
где et - остаточная величина, связанная с наблюдением в момент времени t.
Для интерпретации статистических данных можно следовать правилам, описанным на рис.
# Test for Autocorrelated Errors
durbinWatsonTest(fitted_Model_multiple)
lag Autocorrelation D-W Statistic p-value
1 -0.03814535 2.076011 0.192
Alternative hypothesis: rho != 0
#ACF Plots
plot(acf(fitted_Model_multiple$residuals))
График на рис. называется графиком автокорреляционной функции (ACF) для различных лагов. Этот график популярен при анализе временных рядов, поскольку данные являются временными индексами. Статистика Дурбина Уотсона не показывает автокорреляции между остатками, при этом d равно 2,07. Также на графиках ACF не видно всплесков. Следовательно, можно сказать, что остатки не подвержены автокорреляции.
Гомоскедастичность
Гомоскедастичность означает, все случайные переменные в последовательности или векторе имеют конечную и постоянную дисперсию. Это также называется однородностью дисперсии. В рамках линейной регрессии гомоскедастичные ошибки / остатки будут означать, что дисперсия ошибок не зависит от значений X. Это означает, что распределение вероятности имеет одинаковое стандартное отклонение независимо от X. Существует несколько статистических испытаний для проверки предположения гомоскедастичности, например, Тест Бреша-Пагана, тест арки, тест Бартлетта. Рассмотрим тест Бартлетта, разработанному в 1989 году Снедекором и Кокраном. Для выполнения теста Бартлетта, сначала создаем подгруппы в данных выборки. Например, три группы популяционных данных с 400, 400 и 269 наблюдениями в каждой группе. Можно создать три группы в данных, чтобы увидеть, варьируется ли дисперсия по этим трех группам GP <-NUMERIC () 294
gp<-numeric()
for( i in 1:1069)
{
if(i<=400){
gp[i] <-1;
}else if(i<=800){
gp[i] <-2;
}else{
gp[i] <-3;
}
}
Теперь мы определяем гипотезу, которую будем проверять с помощью теста Бартлетта:
H0(нулевая гипотеза): Все три дисперсии в популяции одинаковы.
HА(альтернативная гипотеза): По крайней мере, две из них отличаются друг от друга.
Здесь мы выполняем тест Бартлетта с помощью функцииBartlett.test():
Data_lm_Model$gp <-factor(gp)
bartlett.test(fitted_Model_multiple$fitted.values,Data_lm_Model$gp)
Bartlett test of homogeneity of variances
data: fitted_Model_multiple$fitted.values and Data_lm_Model$gp
Bartlett's K-squared = 1.3052, df = 2, p-value = 0.5207
Критерий Бартлетта имеет значение p, превышающее 0,05, что означает, что мы не можем отвергнуть нулевую гипотезу. Подгруппы имеют одинаковую дисперсию, и, следовательно, дисперсия гомоскедастична.
Приведем еще несколько тестов для проверки дисперсий.
# 1. Breush-Pagan Test
# non-constant error. variance test - breush pagan test
ncvTest(fitted_Model_multiple)
Non-constant Variance Score Test
Variance formula: ~ fitted.values
Chisquare = 2322.866 Df = 1 p = 0
# 2. ARCH Test
#also show ARCH test - More relevant for a time series model
Install.packages("FinTS")
library(FinTS)
ArchTest(fitted_Model_multiple$residuals)
ARCH LM-test; Null hypothesis: no ARCH effects
data: fitted_Model_multiple$residuals
Chi-squared = 4.2168, df = 12, p-value = 0.9792
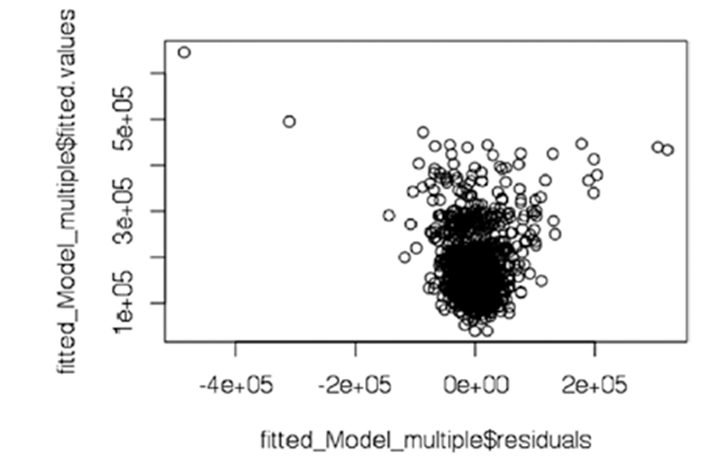
Результаты теста Бартлетта и теста Arch ясно показывают, что остатки гомоскедастичны. График на рисунке представляет собой зависимость остатков от установленных значений. Это точечный график отклонений по оси x и подобранных значений (оценочных откликов) по оси y.
График используется для выявления нелинейности, неравномерных отклонений ошибок и выбросов.
# plot residuals vs. fitted values
plot(fitted_Model_multiple$residuals,fitted_Model_multiple$fitted.values)
Оценка модели - самый важный шаг в разработке любого решения для машинного обучения. На этом этапе разработки модели мы оцениваем производительность модели и решаем, продолжать ли работу с моделью или вернуться ко всем нашим предыдущим шагам в процессе машинного обучения. Во многих случаях мы можем даже отказаться от полной модели, основанной на показателях производительности. Основная идея оценки модели заключается в минимизации ошибок в тестовых данных, где ошибку можно определить по-разному. В самом понятном смысле ошибка - это разница между фактическим значением переменной-предиктора в данных и значением , которое предсказывает ML-модель. Показатели ошибок не всегда универсальны, и для решения некоторых специфических задач требуются креативные показатели ошибок, соответствующие задаче и знаниям предметной области. Здесь важно подчеркнуть, что показатель ошибок, используемый для обучения модели, может отличаться от показателя ошибок оценки. Например, для модели классификации можно использовать метрику ошибок LogLoss, но для оценки модели можно также вывести коэффициент классификации с использованием матрицы путаницы.
Выведем типы переменных исходного набора данных (цена на дом)
install.packages ("data.table")
library(data.table)
Data_House_Price <-fread("Dataset/House Sale Price Dataset.csv",header=T,
verbose =FALSE, showProgress =FALSE)
str(Data_House_Price)
Classes 'data.table' and 'data.frame': 1300 obs. of 14 variables:
$ HOUSE_ID : chr "0001" "0002" "0003" "0004" ...
$ HousePrice : int 163000 102000 265979 181900 252000 180000 115000
176000 192000 132500 ...
$ StoreArea : int 433 396 864 572 1043 440 336 486 430 264 ...
$ BasementArea : int 662 836 0 594 0 570 0 552 24 588 ...
$ LawnArea : int 9120 8877 11700 14585 10574 10335 21750 9900
3182 7758 ...
$ StreetHouseFront: int 76 67 65 NA 85 78 100 NA 43 NA ...
$ Location : chr "RK Puram" "Jama Masjid" "Burari" "RK Puram" ...
$ ConnectivityType: chr "Byway" "Byway" "Byway" "Byway" ...
$ BuildingType : chr "IndividualHouse" "IndividualHouse"
"IndividualHouse" "IndividualHouse" ...
$ ConstructionYear: int 1958 1951 1880 1960 2005 1968 1960 1968 2004 1962
...
$ EstateType : chr "Other" "Other" "Other" "Other" ...
$ SellingYear : int 2008 2006 2009 2007 2009 2006 2009 2008 2010 2007
...
$ Rating : int 6 4 7 6 8 5 5 7 8 5 ...
$ SaleType : chr "NewHouse" "NewHouse" "NewHouse" "NewHouse" ...
- attr(*, ".internal.selfref")=<externalptr>
Далее представлена сводная информация о цене продажи дома. Это
наша зависимая переменная.
dim(Data_House_Price)
[1] 1300 14
Проверка распределения зависимой переменной ( House Price). Вывод гистограммы
hist(Data_House_Price$HousePrice/1000000, breaks=20, col="blue", xlab="House
Sale Price(Million)",
main="Distribution of House Sale Price")
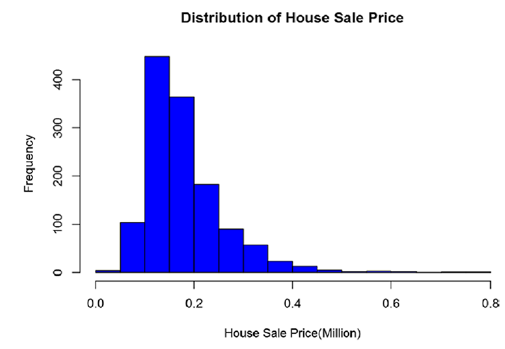
Здесь мы вызываем функцию summary(), чтобы просмотреть основные свойства данных о ценах на жилье. На
выходе мы получаем минимум, первый квартиль, медиану, среднее значение, третий квартиль и максимум.
summary(Data_House_Price$HousePrice)
Min. 1st Qu. Median Mean 3rd Qu. Max.
34900 129800 163000 181500 214000 755000
#Pulling out relevant columns and assigning required fields in the dataset
Data_House_Price <-Data_House_Price[,.(HOUSE_ID,HousePrice,StoreArea,StreetHouseFront,BasementArea,LawnArea,Rating,SaleType)]
Следующий фрагмент кода удаляет недостающие значения из набора данных. Этоважно для обеспечения согласованности всех данных.
#Omit Any missing value
Data_House_Price <-na.omit(Data_House_Price)
Data_House_Price$HOUSE_ID <-as.character(Data_House_Price$HOUSE_ID)
V. Оценка производительности модели
Оценка производительности выполняются, после того, как модель разработана и необходимо понять, как модель работает на тестовых/валидационных данных. Перед началом разработки модели данные обычно делятся на три категории:
1. Training Data (данные для обучения): Этот набор данных используется для обучения модели / машины. На этом этапе фокус алгоритма обучения сосредоточен на том, чтобы оптимизировать некоторую четко определенную метрику, отражающую суть модели. Например, в QLS, используются данные для обучения модели линейной регрессии путем минимизации квадратичных ошибок.
2. Testing Data (тестовые данные): Тестовый набор данных содержит точки данных, которые алгоритм ML не видел ранее. Мы применяем этот набор данных, чтобы увидеть, как модель выполняет новых данных. Большая часть оценки производительности модели рассчитываются на этом этапе. Здесь принимается решение об улучшениях модели и внесении в нее изменений.
3. Validation dats: ( проверочные данные) : цель этого набора данных состоит в том, чтобы проверить переобучение модели и оценить необходимость калибровки. Если не удасться откалибровать модель, то весь процесс начнется заново.
Для достаточно больших данных, которые можно использовать в соотношении 60:20:20 для обучения, тестирования и валидации. Модель производительности измеряется с помощью тестовых данных, и разработчик решает, какие пороговые значения приемлемы для подгонки модели. Метрики производительности в целом генерируются с использованием основных критериев подгонки модели и результаты несколько отличаются от фактического вы-ода модели. Эта ошибка между фактическими и предсказанными данными должна быть минимизирована для хорошей производительности. Часто используемые показатели производительности и оценки применяются для двух типов переменных выхода модели (предикторов):
- Непрерывный вывод: модель или серия моделей, которые дают непрерывное предсказанное значение для непрерывной зависимой переменной в модели. Например, HousePrices является непрерывной и, при использовании для прогнозирования модели, будет давать непрерывные прогнозируемые значения.
- Дискретный выход: модель или серия моделей, которые дают дискретное предсказанное значение для дискретной зависимой переменной в модели. Например, для приложения кредитной карты, класс риска заемщика при использовании в прогностической модели для классификации приведет к дискретной предсказанной цене (прогнозируемый класс риска).
Можно классифицировать параметры оценки модели следующим образом:
Точность: Точность модели отражает долю правильных прогнозов - в непрерывном случае, ее минимальный остаток, и в дискретных, правильность прогноза класса, минимальный остаток в непрерывных случаях или несколько неверных классификаций в дискретных случаях подразумевает более высокую точность и лучшую модель.
Выигрыши: статистика получения дает нам представление о производительности самой модели. Сравнивается модель вывода с результатом, который получен без использования модели (или с помощью случайной модели). Таким образом можно сравнить модель с случайной моделью, которая дает случайный исход. При сравнении двух моделей предпочтение отдается модели с более высокой статистикой прироста в определенном процентиле.
Аккредитация: Аккредитация модели отражает достоверность модели для фактического использования. Этот подход гарантирует, что данные, на которых применяется модель, аналогична данным для обучения. Индекс устойчивости выборки является одной из мер для обеспечения аккредитации перед использованием модели. Индекс устойчивости выборки - это мера, чтобы выяснить, будет ли набор данных по модельной подготовке относительно данных, когда используется модель, или выборка стабильны относительно функций, используемых в модели. Значение индекса варьируется от 0 до 1, с высокими значениями, указывающими на большее сходство между предикторами в двух наборах. Стабильная популяция подтверждает использование модели для прогнозирования.
Стабильность выборки редко игнорируется при тестировании производительности модели на различных наборах данных. Идея состоит в том, чтобы гарантировать, что набор данных тестирования совпадает с набором данных обучения. Если это так, то модель производительности дает представление о том, насколько хорошо выполнена модель. В противном случае полученные результаты производительности модели бесполезны
Разделим данные выборки на две части, скажем, Set 1 и Set 2. 1 - в качестве данных для обучения 2 - в качестве данных для тестирования.
#Create set 1 and set 2 : 2/3 данных на set 1 и остальные 1/3 на set 2
summary(Data_House_Price$HousePrice)
Min. 1st Qu. Median Mean 3rd Qu. Max.
34900 127500 159000 181300 213200 755000
set_1 <-Data_House_Price[1:floor(nrow(Data_House_Price)*(2/3)),]$HousePrice
summary(set_1)
Min. 1st Qu. Median Mean 3rd Qu. Max.
34900 128800 160000 180800 208900 755000
set_2 <-Data_House_Price[floor(nrow(Data_House_Price)*(2/3) +1):nrow(Data_
House_Price),]$HousePrice
summary(set_2)
Min. 1st Qu. Median Mean 3rd Qu. Max.
52500 127000 155000 182200 221000 745000
Для непрерывного случая мы можем проверить устойчивость, используя двух параметрический тест KS (непараметрический тест для сравнения совокупного распределения двух образцов).
Статистика KS дает наибольшее значение разницы между эмпирическим сравнением распространения двух образцов и, если оно высоко, то мы говорим, что два образца различны. С точки зрения стабильности выборки, тест сообщает, что модель производительности не может быть измерена на новых образцах, а базовый образец не из того же распределения, на котором была обучена модель.
Определим функцию ks_test (), которая строит Empirical Cumulative Distribution Function (ECDF) и отображает результат теста KS.
#Defining a function to give ks test result and ECDF plots on log scale
install.packages("rgr")
library(rgr)
ks_test <-function (xx1, xx2, xlab ="House Price", x1lab=deparse(substitute(xx1)), x2lab =deparse(substitute(xx2)), ylab ="Empirical
Cumulative Distribution Function",log =TRUE, main ="Empirical EDF Plots -
K-S Test", pch1 =3, col1 =2, pch2 =4, col2 =4, cex =0.8, cexp =0.9, ...)
{
temp.x <-remove.na(xx1)
x1 <-sort(temp.x$x[1:temp.x$n])
nx1 <-temp.x$n
y1 <-((1:nx1) -0.5)/nx1
temp.x <-remove.na(xx2)
x2 <-sort(temp.x$x[1:temp.x$n])
nx2 <-temp.x$n
y2 <-((1:nx2) -0.5)/nx2
xlim <-range(c(x1, x2))
if (log) {
logx <- "x"
if (xlim[1] <=0)
stop("\n Values cannot be .le. zero for a log plot\n")
}
else logx <- ""
plot(x1, y1, log = logx, xlim = xlim, xlab = xlab, ylab = ylab,
main = main, type ="n", ...)
points(x1, y1, pch = pch1, col = col1, cex = cexp)
points(x2, y2, pch = pch2, col = col2, cex = cexp)
temp <-ks.test(x1, x2)
print(temp)}
Здесь выполняется KS test на set_1 and set_2 и выводится ECDF.
#Perform K-S test on set_1 and set_2 and also display Empirical Cumulative
Distribution Plots
ks_test(set_1,set_2)
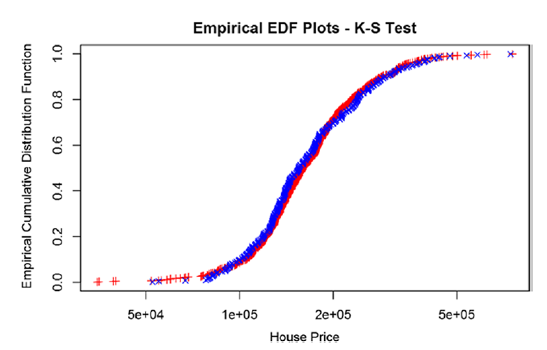
Здесь показаны результаты проверки гипотезы для теста KS. Это тест Колмогорова-Смирнова для проверки гипотезы о том, что оба распределения были получены из одного и того же базового распределения.
Two-sample Kolmogorov-Smirnov test
data: x1 and x2
D = 0.050684, p-value = 0.5744
alternative hypothesis: two-sided
Тест Колмогорова - Смирнова для гипотезы, которую оба распределения были привлечены из того же основного распределения.
Тестовые данные: x1 и x2 d = 0,050684, p-значение = 0,050684, p-значение = 0.5744
Альтернативная гипотеза: двусторонняя. Значение p составляет более 0,05, и мы не отказываемся от нулевой гипотезы. Таким образом, мы далее нужно тестировать модель производительности на тестовых данныех. Глядя на график эмпирической кумулятивной функции распределения (ECDF), можно видеть, что ECDF для обоих образцов одинаково, и, следовательно, они происходят из одного и того же распределения выборки.
Как выглядит результат, когда выборка нестабильна? Пусть набор 2 был подвержен изменениям, где дома были обложены дополнительным налогам местным органом и, следовательно, цены выросли. Может ли существующая модель все еще хорошо работать на этом новом наборе?
#Manipulate the set 2
set_2_new <-set_2*exp(set_2/100000)
#Снова проведем k-s тест
ks_test(set_1,set_2_new)
Теперь построим ECDF для набора 1 и набора 2 и сравним с предыдущим результатом.
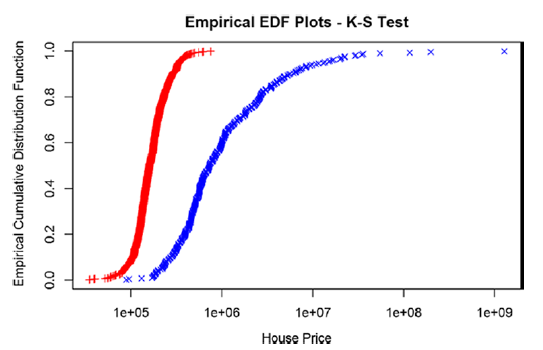
Двухвыборочный Kolmogorov-Smirnov test
data: x1 and x2
D = 0.79957, p-value < 2.2e-16
alternative hypothesis: two-sided
P-значение KS теста составляет менее 0,05, и, следовательно, тест отвергает нулевую гипотезу: оба образца относятся к одной и той же выборке.
Визуально графики ECDF отличаются друг от друга. Следовательно, модель не может быть использована на новом наборе данных. .
Оценка модели для получения непрерывного результата
Распределение зависимых переменных является важным соображением при выборе методов для оценки моделей. Интуитивно, мы в конечном итоге сравниваем остаточное распределение (фактическое значение прогнозируемого значения) с нормальным распределением (то есть, случайным шумом) или каким-либо другим распределением на основе метрик, которые мы выбираем.
Рассчитаем некоторые основные метрики. Метрики имеют собственные достоинства и недостатки.
Установим модель линейной регрессии с переменными, доступными для прогноза цен дома.
# Create a model on Set 1 = Train data
linear_reg_model <-lm(HousePrice ~StoreArea +StreetHouseFront +BasementArea
+LawnArea +Rating +SaleType ,data=Data_House_Price[1:floor(nrow(Data_
House_Price)*(2/3)),])
summary(linear_reg_model)
Call:
lm(formula = HousePrice ~ StoreArea + StreetHouseFront + BasementArea + LawnArea + Rating + SaleType, data = Data_House_
Price[1:floor(nrow(Data_House_Price) * (2/3)), ])
Residuals:
Min 1Q Median 3Q Max
-432276 - 22901 -3239 17285 380300
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -8.003e+04 3.262e+04 -2.454 0.014387 *
StoreArea 5.817e+01 9.851e+00 5.905 5.48e-09 ***
StreetHouseFront 1.370e+02 8.083e+01 1.695 0.090578 .
BasementArea 2.362e+01 3.722e+00 6.346 3.96e-10 ***
LawnArea 7.746e-01 1.987e-01 3.897 0.000107 ***
Rating 3.540e+04 1.519e+03 23.300 < 2e-16 ***
SaleTypeFirstResale 1.012e+04 3.250e+04 0.311 0.755651
SaleTypeFourthResale -3.221e+04 3.678e+04 -0.876 0.381511
SaleTypeNewHouse -1.298e+04 3.190e+04 -0.407 0.684268
SaleTypeSecondResale -2.456e+04 3.248e+04 -0.756 0.449750
SaleTypeThirdResale -2.256e+04 3.485e+04 -0.647 0.517536
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error : 44860 on 701 degrees of freedom
Multiple R-squared: 0.7155, Adjusted R-squared: 0.7115
F-statistic: 176.3 on 10 and 701 DF, p-value: < 2.2e-16
Краткое описание модели показывает несколько особенностей:
• R-square для подогнанной модели составляет 71,5%, что является хорошей подгонкой модели.
• Переменная SaleType незначительна на всех уровнях (но мы сохранили ее в модели, поскольку считаем, что она является важным элементом цены на жилье).
• Значение p для F-теста общего критерия значимости меньше, чем 0,05, поэтому мы можем отвергнуть нулевую гипотезу и заключить, что данная модель обеспечивает лучшее соответствие, чем модель, основанная только на перехвате.
Теперь перейдем к показателям эффективности для непрерывной зависимой переменной.
1. Средняя абсолютная погрешность (MAE)
Средняя абсолютная погрешность или MAE - это один из самых основных показателей погрешности, используемых для оценки
модели. Это средний показатель/среднее значение абсолютной погрешности.
В статистике средняя абсолютная погрешность - это среднее значение абсолютных ошибок:
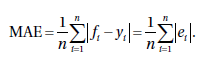
где fi - это прогноз, а yi - истинное значение.
#Создание тестовых данных (set 2)
test <-Data_House_Price[floor(nrow(Data_House_Price)*(2/3) +1):nrow(Data_House_Price),]
#Fit the linear regression model on this and get predicted values
predicted_lm <-predict(linear_reg_model,test, type="response")
actual_predicted <-as.data.frame(cbind(as.numeric(test$HOUSE_ID),as.
numeric(test$HousePrice),as.numeric(predicted_lm)))
names(actual_predicted) <-c("HOUSE_ID","Actual","Predicted")
#Find the absolute residual and then take mean of that
library(ggplot2)
#Plot Actual vs Predicted values for Test Cases
ggplot(actual_predicted,aes(x = actual_predicted$HOUSE_ID,color=Series)) +
geom_line(data = actual_predicted, aes(x = actual_predicted$HOUSE_ID,
y =Actual, color ="Actual")) +
geom_line(data = actual_predicted, aes(x = actual_predicted$HOUSE_ID, y =
Predicted, color ="Predicted")) +xlab('HOUSE_ID') +ylab('House Sale Price')
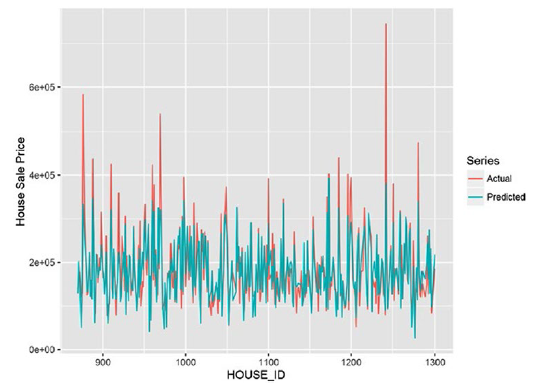
Из графика на рисунке видно, что фактическое значение очень близко к прогнозируемому.
#Remove NA from test, as we have not done any treatment for NA
actual_predicted <-na.omit(actual_predicted)
#First take Actual - Predicted, then take mean of absolute errors(residual)
mae <-sum(abs(actual_predicted$Actual -actual_predicted$Predicted))/nrow(ac
tual_predicted)
cat("Mean Absolute Error for the test case is ", mae)
Mean Absolute Error for the test case is 29570.3
По данным MAE, в среднем погрешность составляет 29, 570 долларов. Это эквивалентно тому, что в долларовом выражении
ожидается погрешность в 17% при среднем значении в 180, 921 доллар.
2. Среднеквадратичная ошибка или RMSE.Среднеквадратичная ошибка или RMSE - один из самых популярных показателей, используемых для оценки
моделей с непрерывными ошибками. Как следует из названия, это квадратный корень из среднеквадратичной
ошибки. Наиболее важной особенностью этой метрики является то, что ошибки взвешиваются путем
возведения их в квадрат. Среднее значение прогнозируемых значений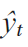 
для моментов времени t зависимой переменной регрессии yt и
вычисляется для n различных прогнозов как квадратный корень из среднего значения квадратов отклонений:
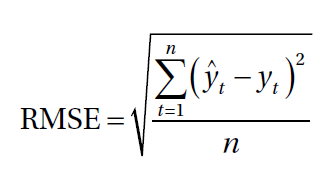
Важно понимать, как операции с метрикой изменяют интерпретацию
показателя. Предположим, что нашей зависимой переменной является цена на жилье, которая выражается в долларах.
Давайте посмотрим, как изменяются параметры метрики для интерпретации показателя.
Прогнозируемое и фактическое значения выражены в долларах, поэтому их разница равна ошибке, опять же в долларах.
Затем вы возводите ошибку в квадрат, и измерение преобразуется в доллар в квадрате. Мы не можем сравнить
значение в долларах в квадрате со значением в долларах. Извлекаем квадратный корень из этого значения, чтобы вернуть измерение к
долларов и теперь можем интерпретировать RMSE в долларовом выражении.
#As we have already have actual and predicted value we can directly calculate the RMSE value
rmse <-sqrt(sum((actual_predicted$Actualactual_predicted$Predicted)^2)/nrow(actual_predicted))
cat("Root Mean Square Error for the test case is ", rmse)
Root Mean Square Error for the test case is 44459.42
Теперь вы можете видеть, что ошибка увеличилась до 44 459 долларов. Это связано с тем, что мы
наказываем модель за далеко идущие прогнозы путем возведения ошибок в квадрат.
Как упоминалось ранее, если вы хотите использовать метрику для сравнения наборов данных или
моделей с разными масштабами, вам необходимо нормализовать ее. Мы
можем сделать то же самое с RMSE, нормализовав ее. Наиболее распространенным способом является деление
RMSE на диапазон или среднее значение:
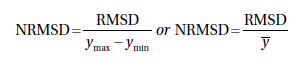
Это значение называется нормализованным среднеквадратичным отклонением или ошибкой
(NRMSD или NRMSE) и обычно выражается в процентах. Низкое значение указывает на меньшую
остаточную дисперсию и, следовательно, является хорошей моделью.
3. R-Square
R-Square - популярный показатель, используемый в методах, основанных на линейной регрессии.
Статистики используют для определения R-квадрата подходящую терминологию - коэффициент детерминации.
Коэффициент детерминации дает представление о взаимосвязи между зависимой переменной (y) и набором независимых переменных (x). В
математической форме это отношение остаточной суммы квадратов к общей сумме квадратов.
Этот показатель также основан на остатке (метрике ошибки) с использованием фактических
и прогнозируемых значений.
#Model training data ( we will show our analysis on this dataset)
train <-Data_House_Price[1:floor(nrow(Data_House_Price)*(2/3)),.(HousePrice,StoreArea,StreetHouseFront,BasementArea,LawnArea,StreetHouseFront,LawnArea
,Rating,SaleType)];
#Omitting the NA from dataset
train <-na.omit(train)
# Get a linear regression model
linear_reg_model <-lm(HousePrice ~StoreArea +StreetHouseFront +BasementArea+LawnArea +StreetHouseFront +LawnArea +Rating +SaleType ,data=train)
# Show the function call to identify what model we will be working on
print(linear_reg_model$call)
lm(formula = HousePrice ~ StoreArea + StreetHouseFront + BasementArea +LawnArea + StreetHouseFront + LawnArea + Rating + SaleType,
data = train)
#System generated Square value
cat("The system generated R square value is " , summary(linear_reg_model)$r.squared)
The system generated R square value is 0.7155461
Текущая линейная модель имеет R-square, равный 0,72. Это может быть истолковано как то, что 72% процентный
разброс в цене дома “объясняется” изменениями предикторов StoreArea, Street House Front, Basement Area, Lawn Area, Street House Front, Lawn Area, Rating, и
Sale Type.
Вычислим R-square
#calculate Total Sum of Squares
SST <-sum((train$HousePrice -mean(train$HousePrice))^2);
#Calculate Regression Sum of Squares
SSR <-sum((linear_reg_model$fitted.values -mean(train$HousePrice))^2);
#Calculate residual(Error) Sum of Squares
SSE <-sum((train$HousePrice -linear_reg_model$fitted.values)^2);
Одним из важных соотношений, которые объединяют эти три суммы квадратов, является
SST = SSR + SSE
Вычисленный R-квадрат совпадает с выводом функции lm().SST = SSR + SSE
Будем использовать эти значения и получим R-square
Оценка модели: R-square для модели:
#calculate R-squared
R_Sqr <-1-(SSE/SST)
#Display the calculated R-Sqr
cat("The calculated R Square is ", R_Sqr)
The calculated R Square is 0.7155461
Можно видеть, что вычисленный R-square совпадает с выводом функции lm().
VI. Вероятностные методы оценки производительности модели
Рассмотрим два метода, соответствующие двум основным группам вероятностных инструментов, которыми располагают специалисты по обработке данных, оба метода основаны на ресемплинге:
• На основе моделирования: K-fold кросс-валидация (перекрестная проверка)
• На основе семплинга: Bootstrap-семплирование
Перекрестная проверка является одним из наиболее часто используемых методов оценки моделей и в последнее время стала признаваться более эффективным методом, чем показатели, основанные на остатках. Проблема с методами, основанными на остаточных данных, заключается в том, что нужно сохранить набор тестов. И этого набора недостаточно, чтобы сообщить, как модель будет вести себя с неизвестными данными. Таким образом, хотя методы обучения, тестирования и валидации хороши, вероятностное моделирование и выборка предоставляют нам больше возможностей для проверки модели.
Перекрестная валидация популярна в сообществе машинного обучения. Чем больше количество кластеров, тем лучше интерпретация
Шаги для выполнения перекрестной проверки:
Шаг 1: Разделите набор данных на k подмножеств.
Шаг 2: Обучите модель на k-1 подмножествах.
Шаг 3: Протестируйте модель на оставшемся подмножестве и вычислите
ошибку.
Шаг 4: Повторяйте шаги 1-3, пока все подмножества не будут использованы для
тестирования ровно по одному разу.
Шаг 5: Усредните ошибки, чтобы получить ошибку перекрестной проверки.
Преимущество этого метода заключается в том, что метод, с помощью которого вы создадите K-подмножеств не так важен по сравнению с ситуацией, когда вы делаете это и на train/test . Кроме того, этот метод гарантирует, что каждая точка данных попадет в тестовыйнабор ровно один раз и в обучающий набор k-1 раз. Дисперсия результирующейоценки уменьшается по мере увеличения k.
Недостатком этого метода является то, что модель должна быть рассчитана k раз, а затем для k-кратного повторения проводится тестирование, что означает более высокую стоимость вычислений (стоимость вычислений пропорциональна количеству к). В одном варианте данные разбиваются случайным образом и контролируетсяр азмер каждого сгиба. Преимущество этого заключается в том, что вы можете самостоятельно выбирать, насколько большим будет каждый набор тестов и сколько испытаний вы пройдете в среднем.
install.packages("caret")
library(caret)
install.packages("randomForest")
library(randomForest)
set.seed(917);
#Данные для обучения модели ( анализ основан на этом наборе данных)
train <-Data_House_Price[1:floor(nrow(Data_House_Price)*(2/3)),.(HousePrice,StoreArea,StreetHouseFront,BasementArea,LawnArea,StreetHouseFront,LawnArea
,Rating,SaleType)];
#Создание тестовых данных(set 2)
test <-Data_House_Price[floor(nrow(Data_House_Price)*(2/3) +1):nrow(Data_
House_Price),.(HousePrice,StoreArea,StreetHouseFront,BasementArea,LawnArea,S
treetHouseFront,LawnArea,Rating,SaleType)]
#Перемещение NA из dataset
train <-na.omit(train)
test <-na.omit(test)
k_10_fold <-trainControl(method ="repeatedcv", number =10, savePredictions=TRUE)
#Подогонка модель по folds, rmse используется в качестве метрики для подгонки модели
model_fitted <-train(HousePrice ~StoreArea +StreetHouseFront +BasementArea+LawnArea +StreetHouseFront +LawnArea +Rating +SaleType, data=train, family
= identity,trControl = k_10_fold, tuneLength =5)
#Вывод статистики по кросс-валидации
model_fitted
Random Forest
712 samples
6 predictor
No pre-processing
Resampling: Cross-Validated (10 fold, repeated 1 times)
Summary of sample sizes: 642, 640, 640, 641, 640, 641, ...
Resampling results across tuning parameters:
mtry RMSE Rsquared
2 40235.04 0.7891003
4 37938.62 0.7961153
6 38049.31 0.7927441
8 38132.67 0.7914360
10 38697.45 0.7858166
RMSE was used to select the optimal model using the smallest value.
The final value used for the model was mtry = 4.
Можно видеть, что модель, выбранная путем перекрестной проверки, имеет более высокий R2, чем та, которую мы создали ранее. Новый R-квадрат равен 80%, а старый был 72%. Также обратите внимание, что по умолчанию для выбора наилучшей модели используется показатель RMSE.
Bootstrap Sampling
Основываясь на случайных выборках из наших данных, мы попытаемся оценить модель и посмотреть, сможем ли мы уменьшить ошибку и получить высокопроизводительную модель. Когда мы используем эти методы в качестве метода оценки производительности, можно заметить, что мы уже настроили модель, т.е. предикторы, и пытаемся определить, что дает наилучшую производительность и в какой степени.
Чтобы показать пример bootstrap, расширим то, что было продемонстрировано для перекрестной проверки.
Возьмем образцы в количестве 10 (т.е. загруженные 10 образцов).
boot_10s <-trainControl(method ="boot", number =10, savePredictions =TRUE)
Fit the model on bootstraps and use rmse as metric to fit the model
model_fitted <-train(HousePrice ~StoreArea +StreetHouseFront +BasementArea
+LawnArea +StreetHouseFront +LawnArea +Rating +SaleType, data=train,
family = identity,trControl = boot_10s, tuneLength =5)
Вывод статистики boost raped model
model_fitted
Random Forest
712 samples
6 predictor
No pre-processing
Resampling: Bootstrapped (10 reps)
Summary of sample sizes: 712, 712, 712, 712, 712, 712, ...
Resampling results across tuning parameters:
mtry RMSE Rsquared
2 40865.52 0.7778754
4 38474.68 0.7871019
6 38818.70 0.7819608
8 39540.90 0.7742633
10 40130.45 0.7681462
RMSE использовался для выбора оптимальной модели через наименьшее значение.
Конечным значением для модели, было mtry = 4.
В случае с bootstrap можно видеть, что наилучшая модель имеет R2, равный 79%, что выше, чем 72% в предыдущем случае, но меньше, чем при 10-кратной перекрестной проверке. Важно отметить, что выборки bootstrap запускаются снова и снова для оценки модели, но перекрестная проверка сохраняет исключительность подмножеств в каждом запуске. Вероятностные методы сложны и их трудно понять. Рекомендуется, чтобы ими пользовался только опытный специалист по обработке данных, поскольку для проведения этих экспериментов требуется глубокое понимание алгоритма машинного обучения и умение правильно интерпретировать их.