Методические указания к лр. 4
Неконтролируемое обучение
Целью алгоритмов неконтролируемого обучения является поиск закономерности в имеющейся информации. Различают следующие алгоритмы неконтролируемого обучения:
- метод k-средних
- метод главных компонент
- астоциативные правила
- анализ социальных сетей
Кластеризация методом k-средних
Кластеризация является методом предварительного
анализа данных. Целью кластеризации является исследование набора данных на
предмет наличия возможных закономерностей. Данные размещаются по группам
(кластерам) в соответствии с подобием
своих признаков.
- Шаг 1: начать с предположения о том, где находятся центры кластеров (центроиды)
- Шаг 2: связать каждый элемент данных с ближайшим центроидом
- Шаг 3: вычислить новое положение центроида, ориентируясь на центр отнесенных к кластеру членов
- Шаг 4: повторять переназначение членов кластера (шаг 2) и eгo репозиционирование (шаг 3) до тех пор, пока все изменения в членстве не прекратятся.
Процесс кластеризации методом k-средних иллюстрируется на рис.
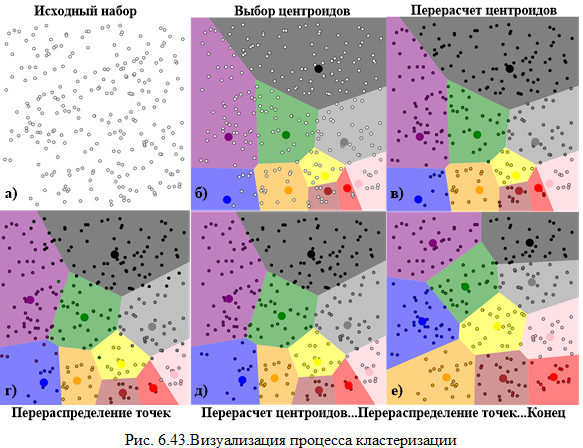
На рис. 6.43 (а) – набор объектов для кластеризации. Затем выбираем первичные центроиды и перераспределяем точки (рис. 6.43 (б). Далее, в цикле, центроиды пересчитываются и обновляются распределения точек. рис. 6.43 (в-д). Процесс останавливается только, когда прекращается перераспределение точек (рис. 6.43 (е)).
Ограничения метода:
- Каждый элемент данных может быть связан только с одним кластером
- Сферичность кластеров. Итеративный процесс поиска ближайшего кластерного центра для элементов данных ограничен его радиусом, поэтому итоговый кластер похож на плотную сферу. Это может стать проблемой, если фактическая форма кластера, например, эллипс. Тогда кластер может быть усечен, а некоторые его члены отнесены к другому кластеру.
- Цельность кластеров. Метод k-средних не допускает того, чтобы они пересекались или были вложены друг в друга.
Определение оптимального количества кластеров
Перед началом кластеризации необходимо определить максимальное количество кластеров. В среде R для этого есть следующие возможности:
- метод локтя
- GAP-статистика
- пакет NbClust
- библиотека vegan
Метод локтя (elbow method) - эвристический метод
График определяет зависимость некоторой величины, характеризующей качество кластеризации, например, внутрикластерной суммы расстояний J от количества кластеров (в статистических пакетах для реализации метода k-средних нужная величина – это искажение или инерция). Оптимальное количество кластеров соответствует значению k, после которого величина J перестает резко падает. Лучший вариант J = 0 достигается при количестве кластеров, совпадающем с числом наблюдений.
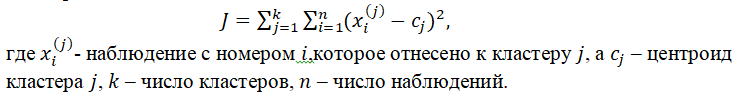
data(Boston)
#метод локтя
install.packages("cluster")
library(cluster)
# Инициализируем переменную, в которую будем записывать fit$tot.withinss
km <- c()
# В цикле проведем кластерный анализ для различного числа кластеров,
# присоединяя к вектору km соответствующие значения
# общей внутрикластерной суммы квадратов
for (k in 1:14) {
fit <- kmeans(Boston, k)
km <- c(km,fit$tot.withinss)}
# Построим график (тип - сплошная линия) по значениям вектора km
# в type используется литера «l»(не цифра 1)
plot(km, type="l")
# Нанесем на график маркеры точек (рис. 6.44)
points(km, pch=2)
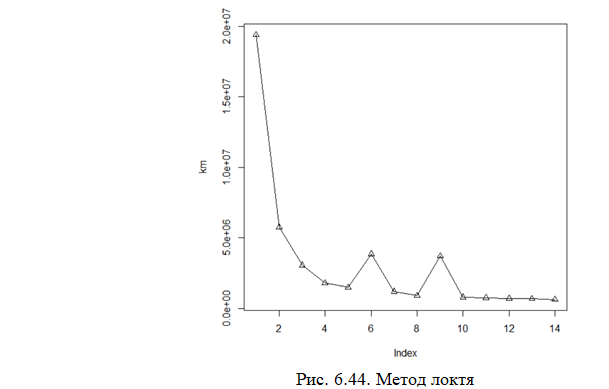
Рекомендованное количество кластеров по графику - ³10, так как 10 является крайним левым значением по оси x, после которого не происходит уменьшение значения по оси y.
6.3.1.2.Метод GAP-статистики
set.seed(123)
#подключить пакет cluster
df.stand<-as.data.frame(scale(Boston))
gap_stat <- clusGap(df.stand, FUN = kmeans, nstart = 10,
K.max = 10, B = 50)
# Печать и визуализация результатов
print(gap_stat, method = "firstmax")
Результат работы метода представлен на рис. 6.45.

Визуализируем результаты (рис. 6.46):
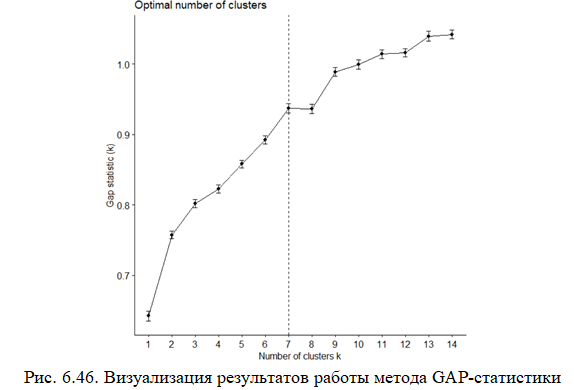
install.packages("factoextra")
library(factoextra)
fviz_gap_stat(gap_stat, linecolor = "black")+ geom_vline(xintercept = 0, linetype = 2)
#функция кластеризации методом k-средних
k.pam<-pam(df.stand,k=7)
#вычисление силуэтов
fviz_silhouette(silhouette(k.pam))
Привязка к кластерам оценивается при помощи силуэта, величины, вычисляемой по формуле:
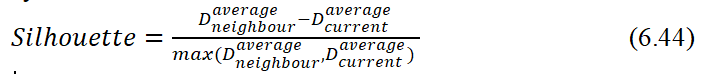
Результат расчета силуэта по каждому участнику кластеризации может принимать значения от –1 до 1:
1 - кластеры выбраны верно
0 - кластеры выбраны неверно
< 0 - соседний кластер больше подходит.
Силуэт – показатель, независимый от k (количество кластеров в методе k-средних.
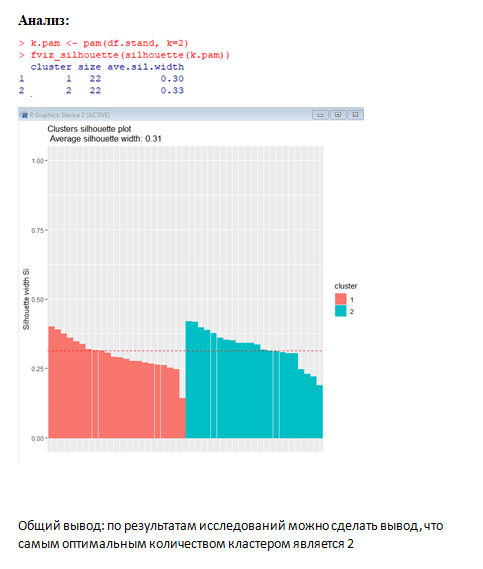
Диаграмма силуэтов при разбиении на 7 кластеров приведена на рис. 6.47.
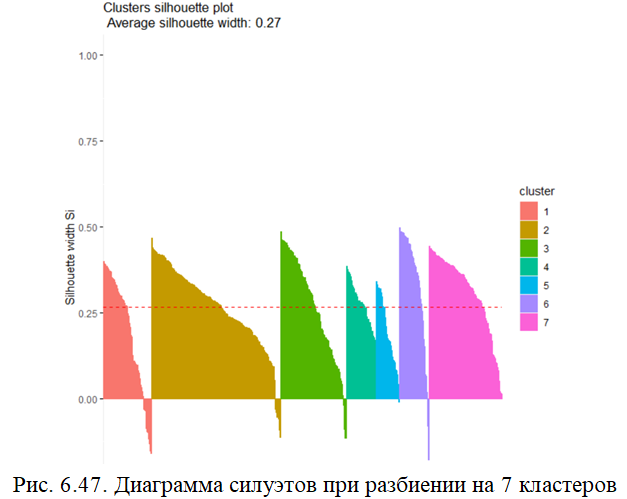
На графике для каждого из объектов показана разность s средних расстояний до объектов своего класса и чужого кластера, ближайшего к анализируемому объекту. Общее среднее из этих значений Smean определяет качество выполненной кластеризации.
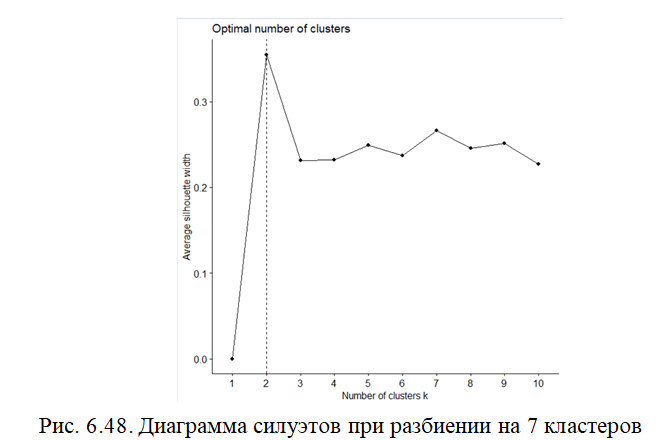
Функция fviz_nbclust() cканирует разбиение с различными значениями k и строит график зависимости Smean (среднее значение генеральной совокупности) от k (рис. 6.48):
fviz_nbclust(df.stand, pam, method = "silhouette", linecolor = "black")+ geom_vline(xintercept = 0, linetype = 2)
Метод NbClust
Метод осуществляет расчет по 30 индексам для определения количества кластеров, а также удобную эффективную схему кластеризации на основе различных комбинаций количества кластеров, мер расстояний и методов кластеризации.
install.packages("NbClust")
library(NbClust)
nb <- NbClust(df.stand, distance = "euclidean", min.nc = 2, max.nc = 8, method = "average", index = "all")
nb$Best.nc
На рис. приведен результат расчета рекомендованного количества кластеров для данного набора. Каждая из строк содержит рекомендованное некоторыми из 30 индексов число кластеров. Наибольшее количество индексов (6) рекомендует использовать при кластеризации по 3 кластерам (рис. 6.49, 6.50)

Результаты предыдущего расчета подтверждаются графически (рис.6.51, 6.52). На обоих графиках самое большое колено (его верхняя точка), соответствует значению 3 по оси x – 3 кластерам.
#визуализация расчетов метода NbClust
fviz_nbclust(nb) + theme_minimal()
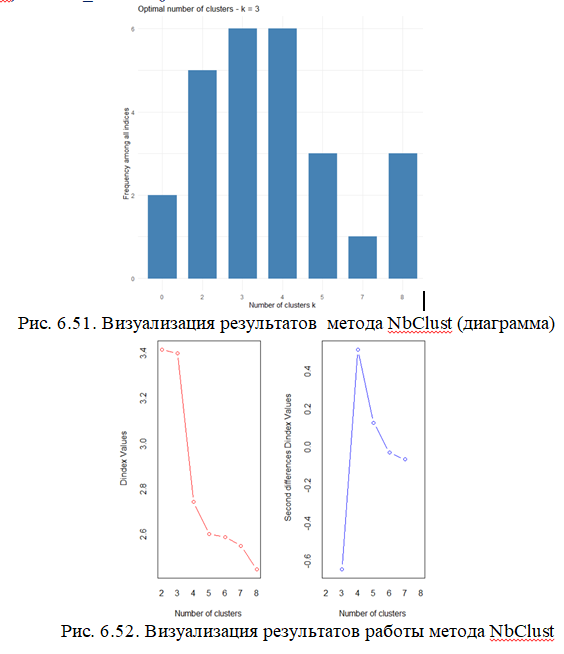
Индекс D (Dindex Value) - это графический метод определения количества кластеров.
На левом графике индекса D мы ищем значительное отклонение (отрезок от 3 до 4 кластера). На графике справа - значительный пик в индексе (рост от 3 до 4 кластера). Это соответствует рекомендации на рис. 6.49 - 3 кластера.
Библиотека Vegan
Кофенетическую корреляция - мера адекватности кластерного решения по исходным данным рассчитывается по исходной матрице расстояний и матрицей кофенетических расстояний. Оценим по этому показателю пять иерархических кластеризаций.
#определение и визуализация оптимального количества кластеров
df.stand<-as.data.frame(scale(Boston))
d <- dist(df.stand, method = "euclidean")
library(vegan)
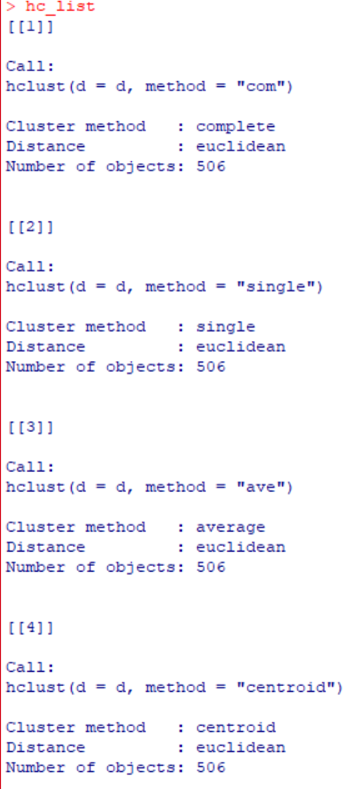
hc_list <- list(hc1
<- hclust(d,"com"),
hc2 <- hclust(d,"single"),
hc3 <- hclust(d,"ave"),
hc4 <- hclust(d,
"centroid"), hc5 <- hclust(d,
"ward.D2"))
hc_list

Coph <- rbind( MantelStat <- unlist(lapply(hc_list, function(hc) mantel(d, cophenetic(hc))$statistic)), MantelP <- unlist(lapply(hc_list, function(hc) mantel(d, cophenetic(hc))$signif)))
colnames(Coph) <- c("Complete", "Single", "Average", "Centroid", "Ward.D2")
rownames(Coph) <- c("W Mantel", "Р-значение")
round(Coph, 3)
На рис.6.53 приведен результат расчета характеристик для пяти методов кластеризации.

Таким образом, максимальное значение коэффициента W матричной корреляции Мантеля (а, следовательно, и наибольшая адекватность матрице расстояний, построенной по исходным данным) для рассматриваемого обучающего набора принадлежит кластеризации методом k-means (average). Все используемые в вычислении методы являются статически значимыми. То есть результаты этих кластеризаций не могут быть случайными.
Еще одна функция библиотеки Vegan – cascadeKM, использует критерий Калински-Харабаса для каскадной кластеризации. Критерий Калински-Харабаса учитывает отношение дисперсии между кластерами к дисперсии внутри кластера (BC / WC).
Несколько k-means кластеризаций, образующих каскад групп, количество кластеров в которых соответствует значениям из диапазона k.
#каскадная кластеризация для набора Boston (рис. 6.55)
model <- cascadeKM(df.stand, 1, 10, iter = 100)
plot(model, sortg = TRUE)
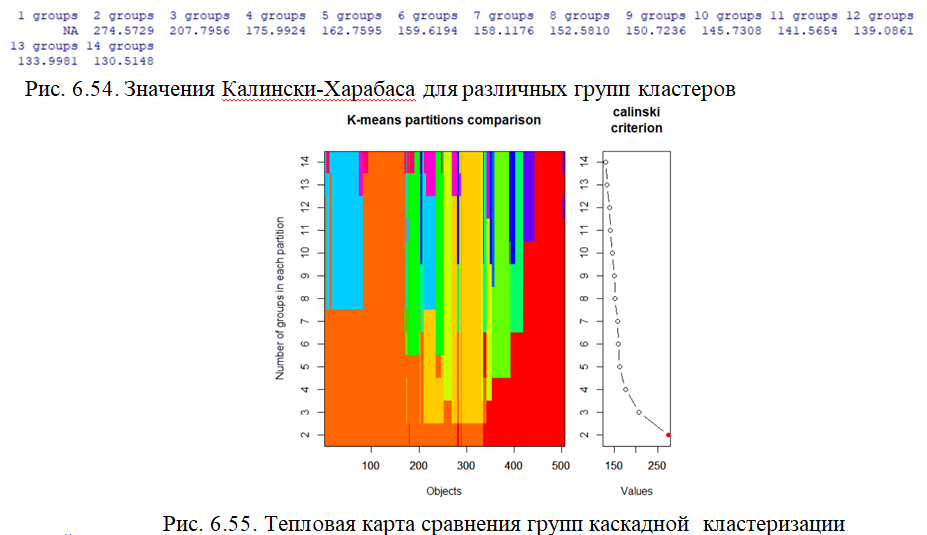
#значения Калински для различных групп кластеров (рис.6.54)
model$results[2,]
#поиск максимального значения BC / WC:
which.max(model$results[2,])
2 группы имеют наибольшее значение BC / WC среди всех (красная точка на графике), поэтому рекомендуемое количество кластеров должно – 2.
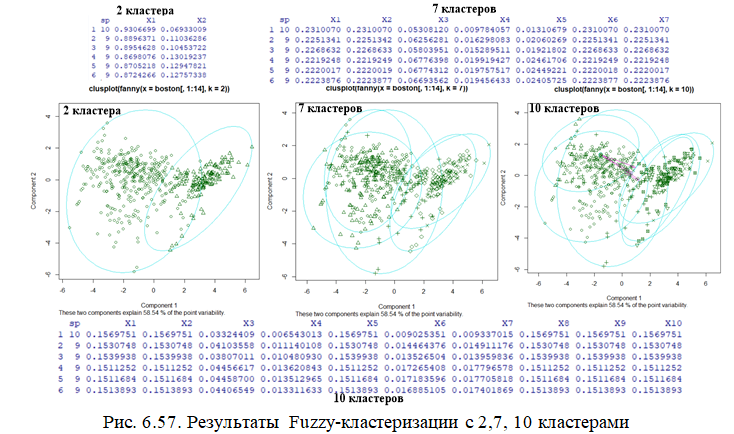
Визуализируем данные, полученные при количестве кластеров, равным 2, 7, 10 (рекомендуемым значениям, полученным при вычислениях) (рис.6.56). Ниже приведен пример кода для количества кластеров – 10 и визуализации по параметрам medv и indus. Для получения результатов, представленных на рис.6.56, необходимо повторить фрагмент кола, изменяя количество кластеров и значения параметров.
#установка пакетов dplyr и ggplot2
install.packages("dplyr")
install.packages("ggplot2")
library(dplyr)
library(ggplot2)
boston<-Boston
#кластеризация с количеством кластеров - 10
fit <- kmeans(boston[,1:14], 10)
boston$clusters <- factor(fit$cluster)
#визуализация результатов относительно значений параметров medv и indus
boston %>%
mutate(clusters = as.factor(clusters)) %>%
ggplot(aes(x = medv, y = indus, fill = clusters)) +
geom_violin() +
coord_flip()
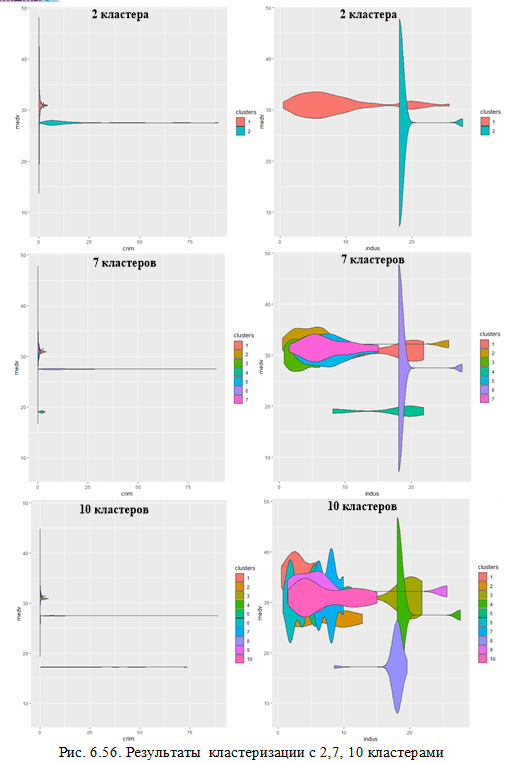
Информация, представленная на рис. позволяет заметить, что независимо от числа кластеров основные тенденции остаются неизменными. Цена на жилье в большой степени зависит от криминогенной обстановки и диапазону показателя индустриализации от 17-18 соответствует самая высокая и самая низкая цена.
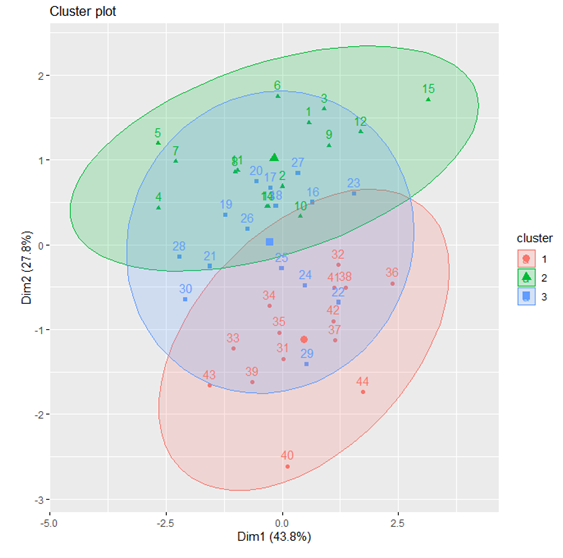
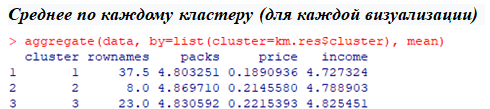
Библиотека factoextra для визуализации рекомендованного методами количества кластеров
В примере ниже рассматривается использование библиотеки factoextra для построения кластеров по рекомендациям методов. Вместо переменной data следует использовать переменную, в которую считывался dataset. В материале выше это переменная boston.
install.packages("factoextra")



Fuzzy-методы кластеризации
Эти методы отражают тот факт, что каждый объект может принадлежать нескольким кластерам сразу, но в разной степени (рис.6.57).
library(cluster)
#функция fanny вычисляет нечеткую кластеризацию в k кластерах
boston.fan <- fanny(boston[,1:14], 7)
plot(boston.fan, which=1)
head(data.frame(sp=boston[,15], boston.fan$membership))
#в строках указывается membership-степень принадлежности объектов кластеру
Таблицы на представленном рисунке в большей степени, чем графический способ визуализации, дают понятие о степени принадлежности объектов к кластерам. Каждая строка таблицы соответствует одному объекту и показывает степень принадлежности этого объекта к каждому кластеру. Рис. показывает, что для количества кластеров больше 2, объекты выборки в большей степени привязаны к крайним кластерам (1,2, 6,7, 8, 9, 10), чем к средним. И степень принадлежности для этих кластеров является одинаковой. При количестве кластеров равном 10, 5-й кластер характеризуется такой же степенью принадлежности, как 1, 2, 8, 9 и 10 кластеры. То есть в целом, характер распределения объектов больше чем по 2 кластерам не привязан к числу кластеров.