Обучение с предпочтением
Рассмотрим пример реализации e-жадной стратегии обучения с предпочтением в среде R.
Целью данного примера является обучение агента оптимальным движениям в лабиринте 2 × 2 (рис. 6.87):
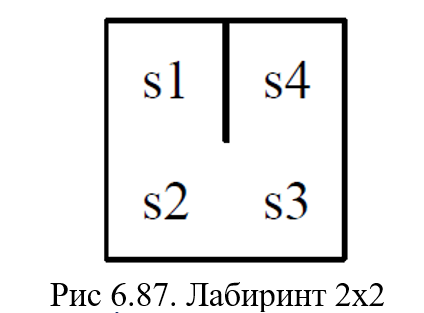
- агент должен найти путь из случайной начальной позиции в некоторую конечную позицию
- каждая ячейка сетки отражает одно состояние s (в общей сложности 4 различных состояния)
- в каждом состоянии агент может выполнить одно из четырех возможных действий: вверх, вниз, влево или вправо в пределах лабиринта
- лабиринт окружен стеной и существует дополнительная стена между состоянием s1 и s4
- вознаграждение оценивается следующим образом:
- каждое движение приводит к отрицательному вознаграждению в размере -1, чтобы штрафовать маршруты, которые не являются кратчайшим путем
- если агент достигнет целевой позиции, он получит вознаграждение в размере 10.
Пример 1.
install.packages("ReinforcementLearning")
library(ReinforcementLearning)
# Определние состояний и действий
states <- c("s1", "s2", "s3", "s4")
actions <- c("up", "down", "left", "right")
Определим функцию, которая имитирует поведение окружающей среды, из которой агент может извлекать свой опыт. Функция принимает в качестве входных данных пару состояние-действие. Состояние относится к положению агента в лабиринте, а действие обозначает предполагаемое движение. На основе этой информации функция принимает решение о следующем состоянии и числовом вознаграждении. Затем она возвращает список, содержащий название следующего состояния и вознаграждение.
#демонстрация кода встроенной функции gridworldEnvironment
env <- gridworldEnvironment
print(env)
function (state, action)
{
next_state <- state
if (state == state("s1") && action == "down")
next_state <- state("s2")
if (state == state("s2") && action == "up")
next_state <- state("s1")
if (state == state("s2") && action == "right")
next_state <- state("s3")
if (state == state("s3") && action == "left")
next_state <- state("s2")
if (state == state("s3") && action == "up")
next_state <- state("s4")
if (next_state == state("s4") && state != state("s4")) {
reward <- 10
}
else {
reward <- -1
}
out <- list(NextState = next_state, Reward = reward)
return(out)
}
После указания функции среды мы можем использовать встроенную функцию sampleExperience() для выборки последовательностей наблюдений из среды.
Функция SampleExperiance() генерирует образец опыта в виде кортежей перехода состояний вида:

Следующий фрагмент кода генерирует 2000 случайных кортежей
# генерация N = 2000 случайных кортежей
data <- sampleExperience(N = 2000,
env = env,
states = states,
actions = actions)
#вывод 19-ти последних из 200 сгенерированных кртежей
tail(data)

# Определение параметров обучения с подкреплением
control <- list(alpha = 0.1, gamma = 0.6, epsilon = 0.2)
# Реализация обучения с подкреплением
model <- ReinforcementLearning(data,
s = "State",
a = "Action",
r = "Reward",
s_new = "NextState",
control = control)
#вывод политики
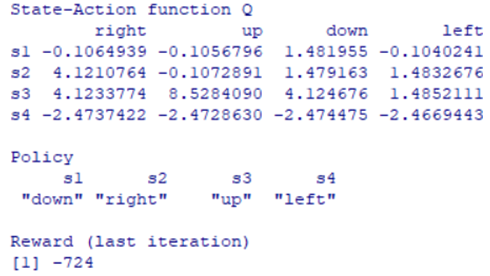
policy(model)
# вывод таблицы состояние-действие
print(model)
# вывод сводной статистики
summary(model)

#выбор новых точек данных из существующей политики с целью получения наилучшего #возможного действия для каждого состояния
data_unseen <- data.frame(State = c("s1", "s2", "s1"),
stringsAsFactors = FALSE)
# Pick optimal action
data_unseen$OptimalAction <- predict(model, data_unseen$State)
data_unseen

На основе полученной информации можно обновить существующую политику.
# генерация N = 1000 случайных кортежей,
# с использованием e -жадной стратегии обучения
data_new <- sampleExperience(N = 1000,
env = env,
states = states,
actions = actions,
actionSelection = "epsilon-greedy",
model = model,
control = control)
# Обновление существующей политики на основе полученных новых данных
model_new <- ReinforcementLearning(data_new,
s = "State",
a = "Action",
r = "Reward",
s_new = "NextState",
control = control,
model = model)
# Вывод результата (рис.6.92)
print(model_new)

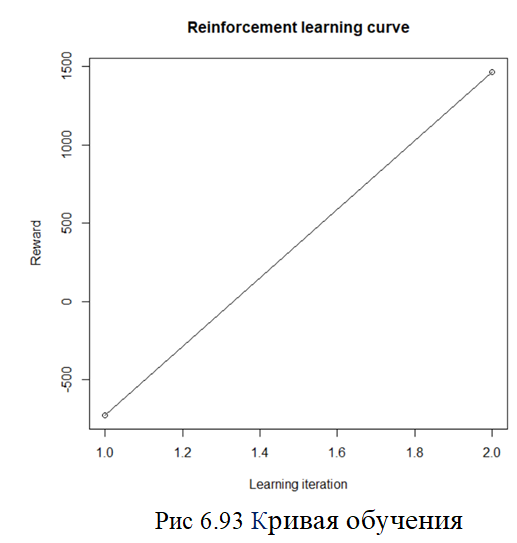
# Plot reinforcement learning curve
plot(model)
# Plot reinforcement learning curve
plot(model_new)
#установка библиотек
install.packages('plot.matrix')
install.packages('RColorBrewer')
library(plot.matrix)
library(RColorBrewer)
# функция, которая создает график R-матрицы с использованием библиотеки plot.matrix
plot_matrix <- function(mat_pot, digits_arg)
{ digits_arg <- ifelse(missing(digits_arg),0,digits_arg)
plot(mat_pot, cex = 1.2, fmt.cell=paste0('%.',digits_arg,'f'),
col=brewer.pal(3,"Accent"), breaks=c(-550, 0, 0, 550),
xlab="States", ylab = "States",main = "")}
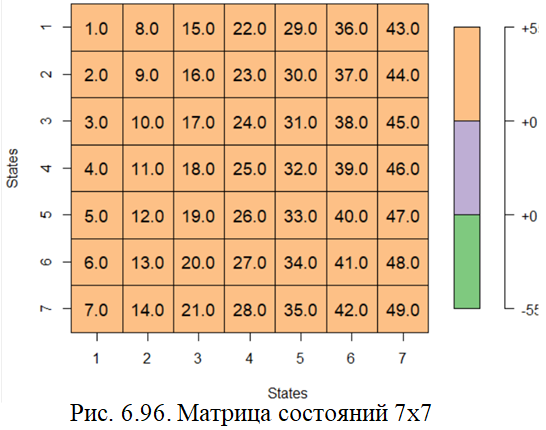
#построение матрицы 7х7 (рис.6.)
states <- seq(1, 7, by = 1)
state_seq <- cbind(merge(states,states), state =
seq(1,length(states)*length(states)))
state_mat <- matrix(state_seq$state, nrow = length(states), ncol= length(states))
plot_matrix(state_mat,1) # (рис. 6.96)
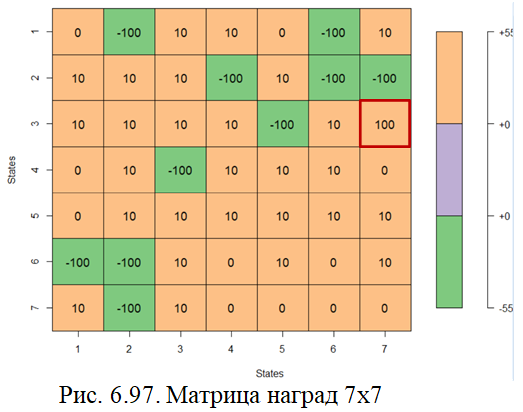
#назначение наград и построение матрицы (рис.6.97)
rewards <- c(0,10,10,0,0,-100,10,
-100,10,10,10,10,-100,-100,
10,10,10,-100,10,10,10,
10,-100,10,10,10,0,0,
0,10,-100,10,10,10,0,
-100,-100,10,10,10,0,0,
10,-100,100,0,10,10,0
)
rewards_mat <- matrix(rewards, nrow = length(states), ncol= length(states))
plot_matrix(rewards_mat)
#установка цели-максимальная награда (клетка 45) выделена красной рамкой
goal <- which(rewards==max(rewards), arr.ind=TRUE)
# Инициализация Q-матрицы – дополнительной матрицы с тем же размером, что и матрица состояний
Q <- matrix(0, nrow = length(states), ncol= length(states))
#код функции getNextState
getNextStates <- function(cs) {
stalen <- length(states);
NS <- stalen*stalen
aa <- state_seq[state_seq$state == cs,]
if (aa$x == max(states)) {
ns <- c(cs - 1,
cs - stalen,
cs + stalen);
} else if (aa$x == min(states)) {
ns <- c(cs + 1,
cs - stalen,
cs + stalen);
} else {
ns <- c(cs + 1,
cs - 1,
cs - stalen,
cs + stalen);
}
#проверка работы функции
nss <- sort(ns[ns > 0 & ns <= NS]);
return(nss);
}
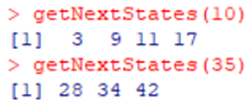
Рис. 6.98. Пример вызова функции определяющий все возможные ходы для заданного состояния
# Серия испытаний – эпизодов, N-количество эпизодов
N <- 20
# Установка параметров обучения:
#alpha – скорость обучения
# gamma – дисконтная ставка
alpha <- 0.9
gamma <- 0.8
for (i in 1:N) {
current_episode <- i;
cat("\nStart Episode: ", current_episode)
## choose next state from possible actions at current state
cs <- sample(state_seq$state, 1)
cat("\n\tCurrent state: ", cs)
step_num <- 1;
while (T) {
cat("\n\n\tStep no.: ", step_num)
cat("\n\t\tCurrent State: ", cs)
reward <- rewards[cs]
if(reward == 0 | is.na(reward) | length(reward) == 0 ){
reward <- 0 }
cat("\n\t\tReward CS: ", reward)
next.states <- getNextStates(cs);
cat("\n\t\tPossible next states: ", next.states)
# next.states
# If we have any states present, else choose randomly.
if (length(next.states) == 1) {
ns <- next.states
} else {
ns <- sample(next.states, 1) }
cat("\n\t\tNext state: ", ns)
# Update Q values for next states.
Q[cs] <- round(Q[cs] + alpha * (reward +
gamma * max(Q[getNextStates(ns)])-Q[cs]),1);
cat("\n\t\tNew Q-Value: ", Q[cs])
plot_matrix(Q,1)
Sys.sleep(3)
if (cs == goal | step_num > 20) {#условие окончания шага эпизода
break;
}
cs <- ns;
step_num <- step_num + 1;
}
cat("\nEnd Episode: ", current_episode)
}
Ниже приведен пример 1-го эпизода из 20, который состоит из 21 шага (рис.6.99). На каждом шаге можно увидеть:
- информацию о текущем состоянии
- награду
- возможные ходы из текущего состояния
- следующее состояние, выбранное агентом из списка возможных
- обновленное значение Q-Value

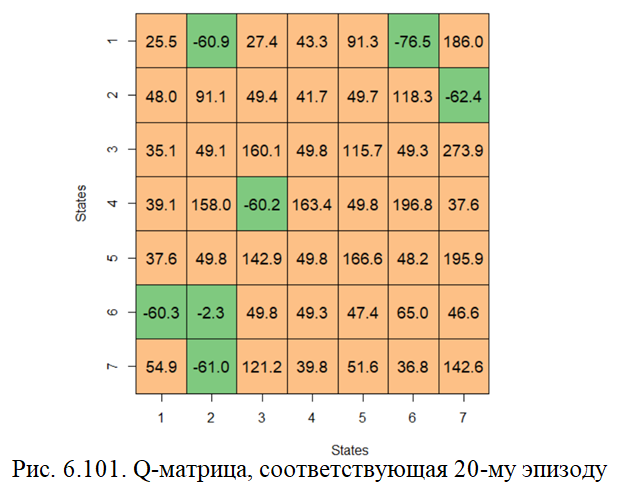
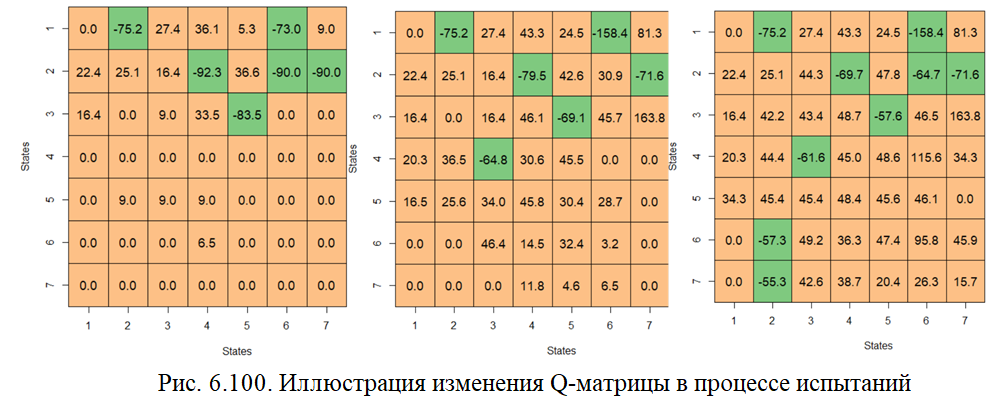
На рис. 6.100 представлены скриншоты, соответствующие разным шагам разных эпизодов, по которым можно заметить изменение изменения Q-матрицы.
На рис. 6.101 приведена Q-матрица, соответствующая последнему, 20-му эпизоду. Можно заметить, в целевой клетке 45 находится максимальное Q-value = 273.9