Технологии машинного обучения (ЛТ): Проверка нулевой гипотезы

Проверка нулевой гипотезы

Нулевая гипотеза

Нулевая гипотеза формулируется в рамках исследования или эксперимента.

Она показывает, что два исследуемых явления никаким образом не связаны друг с другом.

Эксперимент проводится с целью выявить или показать какое-либо влияние или тип

взаимодействия рассматриваемых явлений.

Нулевая гипотеза:

- проверяет отличается ли среднее значение по признаку от

от среднего значения выборки.

(Одновыборочный t-тест)

- Определяет, существует ли существенная разница между средними

значениями двух независимых выборок (Двухвыборочный t-тест).

- Проверяет отличие от нуля средней разницы между парными выборками
(Парный выборочный t-тест)
Примеры нулевой гипотезы (лр.1-регрессионный анализ)

1. Предположение о нормальности распределения остатков. Проверка при помощи

теста Колмогорова-Смирнова (тест KS) и другие тесты. Нулевая гипотеза отклоняется.

2. Все три дисперсии в популяции одинаковы. Проверка при помощи теста Бартлета и др. тестов.

Нулевая гипотеза не отвергается и делается вывод о гомоскедастичности остатков.

3. Нулевая гипотеза о том, что оба распределения были получены из того же основного распределения

Деление данных выборки на две части, Set 1 и Set 2. Set 1 - в качестве данных для обучения Set2 - в качестве

данных для тестирования. Значение p составляет более 0,05, и мы не отказываемся от нулевой гипотезы.

Изменение Set 2 и повторная проверка нулевой гипотезы приводят к ее отвержению.

4. Нулевая гипотеза о лучшей подгонке модели на основе анализа значимости признаков лучшее соответствие, чем модель простая линейна регрессия, основанная только на перехвате.

Для проверки нулевой гипотеpы используются тесты.

В результате теста мы получаем статистику теста и p- значение.
p-value или p-значение – одна из ключевых величин,
используемых в статистике при тестировании гипотез.
Она показывает вероятность получения наблюдаемых
результатов при условии, что нулевая гипотеза верна,
или вероятность ошибки в случае отклонения нулевой гипотезы.
P- значение
P- значение сравнивается с уровнем статистической значимости (альфа).

Обычно альфа имеет значение 0,05 или 0, 01, но возможны и другие значения.

Если p-значение меньше уровня значимости, то нулевую гипотезу можно отклонить и считать истинной альтернативную гипотезу.
```
В этом случае результат эксперимента  является статистически значимым
```

Если p-значение больше уровня значимости, что для отклонения нулевой гипотезы нет достаточных оснований. В этом случае результат эксперимента не является статистически значимым.

Для большинства тестов достаточно статистической значимости, равной 0,05 или 5%.
При этом будет вероятность 95%, что исследователь получил значимый результат вследствие проведенных мероприятий, а не случайно
Используя функцию плотности вероятности, которая связана с нулевой гипотезой, можно

выяснить, удастся ли получить число х (любая метрика) в ходе тестирования (или любое другое значение, которое маловероятнее, чем х) с вероятностью менее 5% (p < 0,05) или менее 1% (p < 0,01), или другого порога, при котором p меньше заданного уровня значимости.

p-критерий отражает вероятность получения результата, который

равен или является более экстремальным, чем фактически наблюдаемый

результат, в случае отсутствия взаимосвязи между исследуемыми переменными.

Проверка гипотез в  Excel
Одновыборочный t-критерий
Одновыборочный t-критерий используется для проверки того, равно ли среднее значение совокупности некоторому значению.
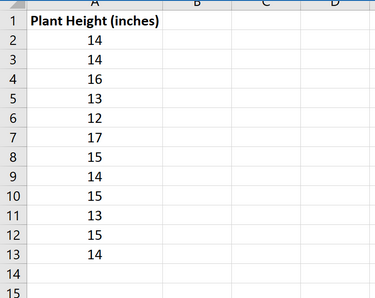
Предположим, исслeдователь хочет знать, равна ли средняя высота определенного вида растения 15 дюймам. Она собирает случайную выборку из 12 растений и записывает их высоту в дюймах.
На следующем изображении показана высота (в дюймах) каждого растения в образце:

Мы можем использовать следующие шаги, чтобы провести t-тест для одной выборки, чтобы определить,

действительно ли средняя высота для этого вида растений равна 15 дюймам.
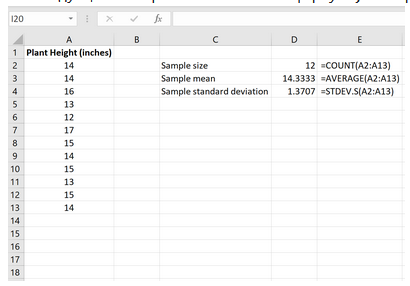
Шаг 1: Найдите размер выборки, среднее значение выборки и стандартное отклонение выборки.
Во-первых, нам нужно найти размер выборки, среднее значение выборки и стандартное отклонение выборки,

которые будут использоваться для проведения одновыборочного t-теста.
На следующем изображении показаны формулы, которые мы можем использовать для расчета этих значений:

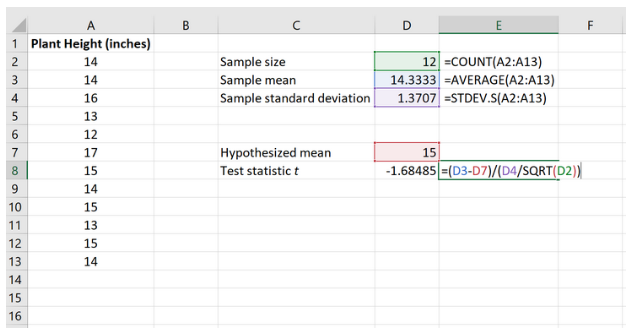
Шаг 2: Рассчитайте тестовую статистику  t .
Далее мы рассчитаем тестовую статистику  t  по следующей формуле:
t  = х - µ / (с / √ п )
где:
x  - выборочное среднее
µ - предполагаемое среднее значение выборки
s - стандартное отклонение выборки
n – размер выборки
Excel:

Тестовая статистика  t  оказывается равной  -1,68485 .
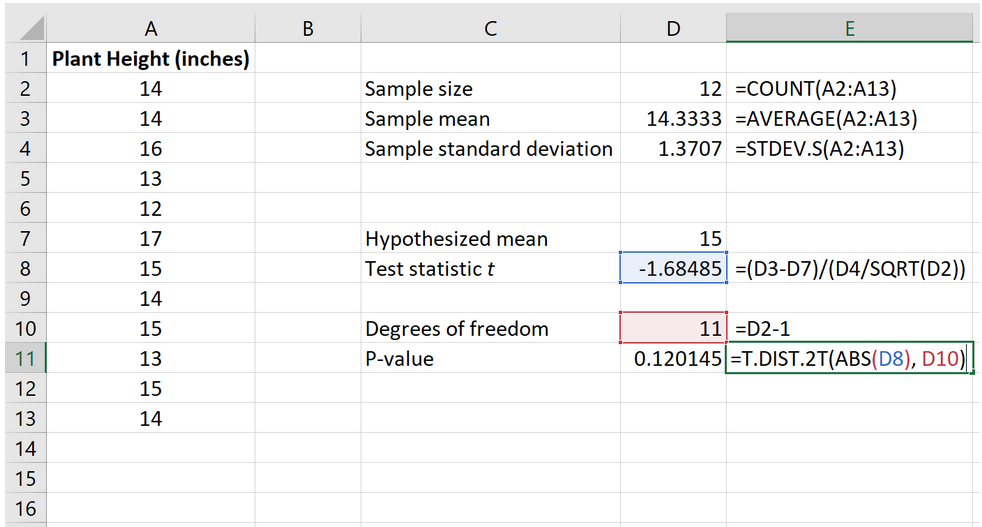
Шаг 3: Рассчитайте p-значение тестовой статистики.
Затем нам нужно рассчитать значение p, связанное со статистикой теста, с помощью функции T.DIST.2T(СТЬЮДЕНТ.РАСП.2Х) в Excel:
=T.DIST.2T(ABS(x), deg_freedom)
где:
x – тестовая статистика t
deg_freedom = степень свободы теста, равная n-1.
Функция T.DIST.2T() возвращает p-значение для двустороннего t-критерия. Если вместо этого используется  левосторонний t-критерий или правосторонний t-критерий, следует  использовать функции T.DIST() или T.DIST.RT() соответственно. Здесь речь идет о типе альтернативной гипотезы.
H ₁ (двусторонняя):  μ ≠ μ ₀ (среднее значение генеральной совокупности не равно некоторому гипотетическому значению μ ₀ )
H ₁ (левосторонняя):  μ < μ ₀ (среднее значение генеральной совокупности меньше некоторого гипотетического значения μ ₀ )
H ₁ (правосторонняя):  μ > μ ₀ (среднее значение генеральной совокупности больше некоторого гипотетического значения μ ₀ )
На следующем изображении показано, как рассчитать p-значение для тестовой статистики:

Значение p оказывается равным  0,120145 .
Шаг 4: Интерпретируйте результаты.
Две гипотезы (нулевая H ₀и альтернативная H _A) для этого конкретного t-критерия с одной выборкой следующие:
H ₀ :  µ = 15 (средняя высота этого вида растений составляет 15 дюймов)
H _A :  µ ≠15 (средняя высота  не  15 дюймов)
Поскольку p-значение нашего теста (0,120145)  больше, чем альфа = 0,05, мы не можем отвергнуть нулевую гипотезу теста.
У нас нет достаточных оснований , чтобы сказать, что средняя высота этого конкретного вида растений отличается от 15 дюймов.
Двухвыборочный t-критерий Стьюдента 
Двухвыборочный t-критерий Стьюдента используется для проверки того, равны ли средние значения двух совокупностей. 
Предположим, исследователи хотят знать, имеют ли два разных вида растений в определенной стране одинаковую среднюю высоту. Поскольку обход и измерение каждого растения заняло бы слишком много времени, они решили собрать образец из 20 растений каждого вида.
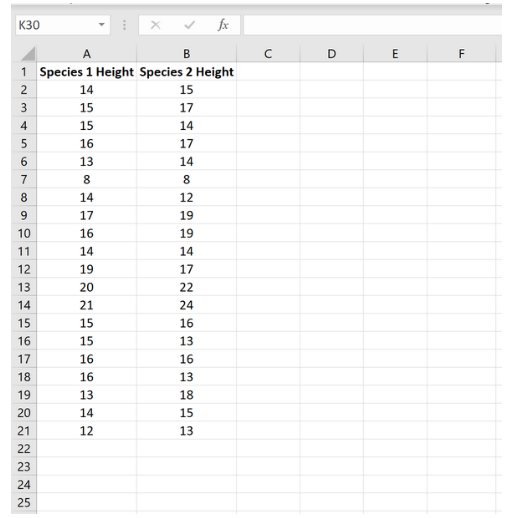
На следующем изображении показана высота (в дюймах) каждого растения в каждом образце:

Мы можем провести двухвыборочный t-тест, чтобы определить, имеют ли два вида одинаковую среднюю высоту, используя следующие шаги:
Шаг 1: Определите, равны ли дисперсии генеральной совокупности . 
Когда мы проводим двухвыборочный t-тест, мы должны сначала решить, будем ли мы предполагать, что две совокупности имеют равные или неравные дисперсии. Как правило, мы можем предположить, что совокупности имеют равные дисперсии, если отношение большей выборочной дисперсии к меньшей выборочной дисперсии составляет менее 4:1. 
Мы можем найти дисперсию для каждого образца, используя функцию Excel  =VAR.S(диапазон ячеек) , как показано на следующем рисунке:

Отношение большей дисперсии выборки к меньшей дисперсии выборки составляет 12,9053 / 8,1342 =  1,586 , что меньше 4. Это означает, что мы можем предположить, что дисперсии генеральной совокупности равны.
Шаг 2: Откройте пакет инструментов анализа .
На вкладке «Данные» на верхней ленте нажмите «Анализ данных».

Если вы не видите этот вариант для выбора, вам необходимо сначала загрузить пакет инструментов анализа.
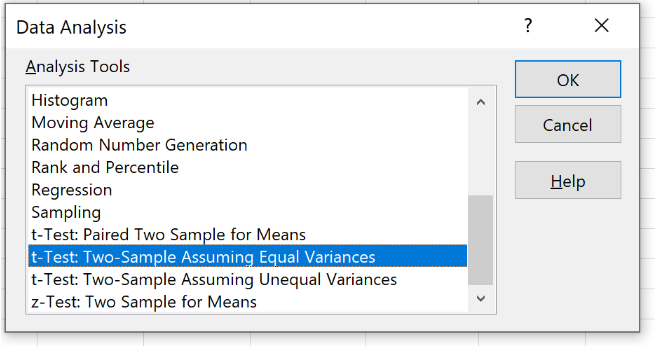
Шаг 3: Выберите подходящий тест для использования.
Выберите вариант с надписью  t-Test: Two-Sample Assassining Equal Variances и нажмите OK.

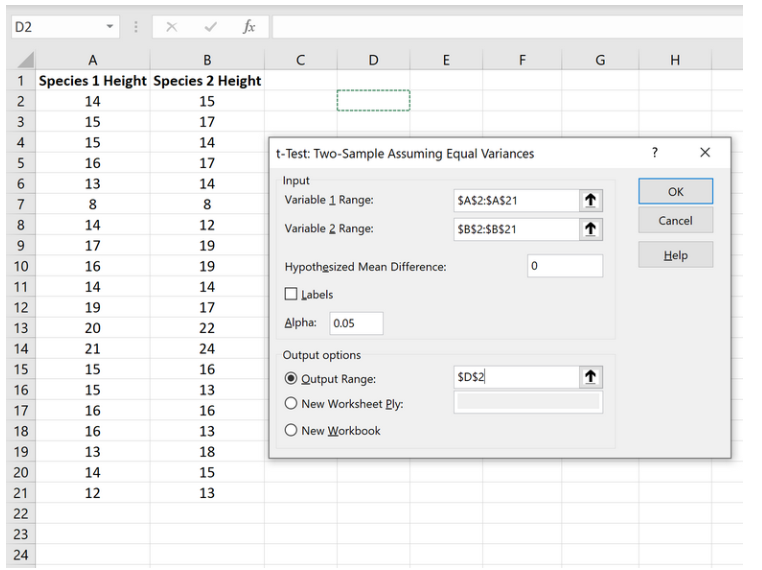
Шаг 4: Введите необходимую информацию .
Введите диапазон значений для переменной 1 (наша первая выборка), переменной 2 (наша вторая выборка), гипотетической средней разницы (в этом случае мы поместили «0», потому что мы хотим знать, равна ли истинная средняя разница генеральной совокупности 0), и выходной диапазон, в котором мы хотели бы видеть результаты t-теста. Затем нажмите ОК.

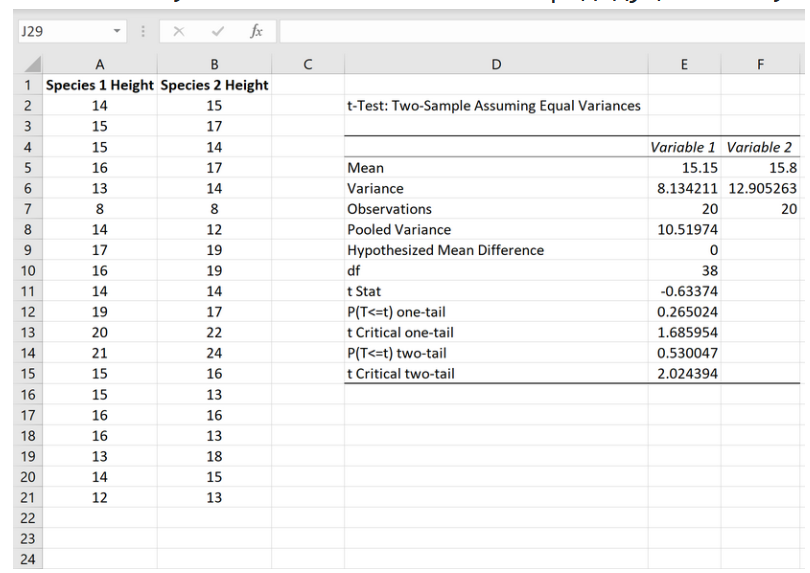
Шаг 5: интерпретируйте результаты .
После того, как вы нажмете OK на предыдущем шаге, отобразятся результаты t-теста. 

Интерпретация результатов:
Среднее значение:  это среднее значение для каждого образца. Образец 1 имеет среднюю высоту  15,15 , а образец 2 имеет среднюю высоту  15,8 .
Дисперсия:  это дисперсия для каждого образца. Выборка 1 имеет дисперсию  8,13  , а выборка 2 —  12,90 .
Наблюдения:  это количество наблюдений в каждой выборке. Обе выборки содержат по 20  наблюдений (например, по 20 отдельных растений в каждой выборке).
Объединенная дисперсия :  Число , которое рассчитывается путем « объединения » дисперсий каждой выборки  вместе по формуле: s²_p = [ (n₁-1)s²₁ + (n₂-1)s²₂ ] / (n₁+n₂-2), что оказывается равным 10,51974 . Это число позже используется при вычислении тестовой статистики  t .
Гипотетическая средняя разница:  число, которое мы «предполагаем», представляет собой разницу между двумя средними значениями совокупности. В данном случае мы выбрали 0 , потому что хотим проверить, равна ли разница между двумя популяциями в среднем 0, например, разницы нет.
df:  Степени свободы для t-критерия, рассчитанные как n ₁ + n ₂ -2 = 20 + 20 – 2 = 38 .
t Stat:  тестовая статистика  t , рассчитанная как  t  = [ x ₁ – x ₂ ] / √ [ s ²_p (1/n ₁ + 1/n ₂ )]
В этом случае t  = [15,15-15,8] / √ [10,51974(1/20+1/20)] =  -0,63374 .
P(T<=t) двухсторонний:  значение p для двустороннего t-критерия. В этом случае р =  0,530047 . Это намного больше, чем альфа = 0,05, поэтому мы не можем отвергнуть нулевую гипотезу. У нас нет достаточных доказательств, чтобы сказать, что два средних значения выборки различны.
t - критический двухсторонний:  это критическое значение теста. У нас - 2,024394 . Поскольку наша тестовая статистика  t  меньше этого значения, мы не можем отвергнуть нулевую гипотезу. У нас нет достаточных доказательств, чтобы сказать, что два средних значения выборки различны. 
 
t-тест для парных выборок (Парный t-критерий Стьюдента)
Критерий Стьюдента  для парных выборок используется для сравнения средних значений двух выборок, когда каждое наблюдение в одной выборке может быть сопоставлено с наблюдением в другой выборке.
Предположим, мы хотим знать, значительно ли влияет определенная учебная программа на успеваемость студента на конкретном экзамене. Чтобы проверить это, у нас есть 20 учеников в классе, которые проходят предварительный тест. Затем каждый из студентов участвует в учебной программе в течение двух недель. Затем учащиеся пересдают тест аналогичной сложности.
Чтобы сравнить разницу между средними баллами по первому и второму тесту, мы используем t-критерий для парных выборок, потому что для каждого учащегося его балл за первый тест можно сопоставить с баллом за второй тест.
На следующем изображении показана оценка до теста и оценка после теста для каждого учащегося:

Выполните следующие шаги, чтобы провести t-критерий для парных выборок, чтобы определить, существует ли значительная разница в средних результатах теста между предварительным тестом и посттестом.
Шаг 1: Откройте пакет инструментов анализа данных.
На вкладке «Данные» на верхней ленте нажмите «Анализ данных».

 
Шаг 2: Выберите подходящий тест для использования.
Выберите вариант с надписью  t-Test: Paired Two Sample for Means и нажмите OK.

Шаг 3: Введите необходимую информацию.
Введите диапазон значений для Переменной 1 (оценки до теста), Переменной 2 (оценки после теста), гипотетической средней разницы (в этом случае мы поместили «0», потому что мы хотим знать, является ли истинная средняя разница между оценки до теста и оценки после теста равны 0), а выходной диапазон, в котором мы хотели бы видеть результаты теста, отображаются. Затем нажмите ОК.

Шаг 4: Интерпретируйте результаты.
После того, как вы нажмете OK на предыдущем шаге, отобразятся результаты t-теста. 

Интерпретация результатов:
Среднее значение:  это среднее значение для каждого образца. Средний балл до теста — 85,4  , а средний балл после теста —  87,2 .
Дисперсия:  это дисперсия для каждого образца. Дисперсия оценок до теста составляет 51,51  , а дисперсия оценок после теста —  36,06 .
Наблюдения:  это количество наблюдений в каждой выборке. Обе выборки имеют по  20  наблюдений.
Корреляция Пирсона:  корреляция между результатами до и после теста. Получается  0,918 .
Гипотетическая средняя разница:  число, которое мы «предполагаем», представляет собой разницу между двумя средними значениями. В данном случае мы выбрали  0  , потому что хотим проверить, есть ли вообще какая-л ибо разница между результатами до и после теста.
df:  Степени свободы для t-критерия. Это рассчитывается как n-1, где n — количество пар. В этом случае df = 20 – 1 = 19 .
t-Stat:  тестовая статистика  t , которая оказывается равной -2,78 .
P(T<=t) двухсторонний:  значение p для двустороннего t-критерия. В этом случае р = 0,011907 . Это меньше, чем альфа = 0,05, поэтому мы отвергаем нулевую гипотезу. У нас есть достаточно доказательств, чтобы сказать, что существует статистически значимая разница между средним баллом до и после теста.
t-критическое двухстороннее:  это критическое значение теста, найденное путем определения значения в  таблице распределения t  , которое соответствует двустороннему тесту с альфа = 0,05 и df = 19. Получается  2,093024 . Поскольку абсолютное значение нашей тестовой статистики  t  больше этого значения, мы отвергаем нулевую гипотезу. У нас есть достаточно доказательств, чтобы сказать, что существует статистически значимая разница между средним баллом до и после теста.
 
Односторонний Z-тест  
 Используется для сравнения наблюдаемой величины с теоретической.
Например, предположим, что телефонная компания утверждает, что 90% ее клиентов удовлетворены их услугами. Чтобы проверить это утверждение, независимый исследователь собрал простую случайную выборку из 200 клиентов и спросил их, довольны ли они своим сервисом, на что 85% ответили утвердительно.
Мы можем использовать односторонний z-тест, чтобы проверить, действительно ли истинный процент клиентов, которые удовлетворены их обслуживанием, составляет 90%.
Алгоритм  выполнения Z-теста
Мы можем использовать следующие шаги для выполнения z-теста одной пропорции:
Шаг 1. Сформулируйте гипотезы. 
Нулевая гипотеза (H0): P = 0,90.
Альтернативная гипотеза: (Ha): P ≠ 0,90
Шаг 2. Найдите статистику теста и соответствующее значение p.
Статистика теста z   = (pP) / (√P(1-P) / n)
где p — доля выборки, P — предполагаемая доля населения, а n — размер выборки.
z = (0,85-0,90) / (√,90 (1-0,90) / 200) = (-,05) / (0,0212) =  -2,358
Используйте калькулятор p-значения для z-оценки -2,358 и двусторонним тестом, чтобы найти, что p-значение =  0,018 .
Шаг 3. Отклонить или не отклонить нулевую гипотезу.
Во-первых, нам нужно выбрать уровень значимости для теста. Обычно выбираются значения 0,01, 0,05 и 0,10. Для этого примера возьмем 0,05. Поскольку p-значение меньше нашего уровня значимости 0,05, мы отвергаем нулевую гипотезу.
Поскольку мы отвергли нулевую гипотезу, у нас есть достаточно доказательств, чтобы сказать, что это неправда, что 90% клиентов удовлетворены их обслуживанием.
 
Пример 1 одновыборочного Z-теста 
Телефонная компания утверждает, что не менее  90% ее клиентов довольны их услугами. Чтобы проверить это утверждение, независимый исследователь собрал простую случайную выборку из 200 клиентов и спросил их, довольны ли они своим сервисом, на что 176 человек ответили утвердительно.
Протестируйте нулевую гипотезу о том, что не менее  90 %  клиентов удовлетворены их обслуживанием, и альтернативную гипотезу о том, что менее 90 % клиентов удовлетворены их обслуживанием. Используйте уровень значимости 0,1. 
На следующем снимке экрана показано, как выполнить односторонний одновыборочный тест z в Excel вместе с используемыми формулами:

Вам нужно заполнить значения для ячеек  B1:B3 . Затем значения для ячеек  B5:B7  автоматически рассчитываются с использованием формул, показанных в ячейках  C5:C7 .
Обратите внимание, что показанные формулы делают следующее:
Формула в ячейке  C5 : рассчитывает долю выборки по формуле Частота / Размер выборки.
Формула в ячейке  C6 : вычисляет статистику теста по формуле (p-P) / (√P(1-P) / n),  где p — доля выборки, P — гипотетическая доля населения, а n — размер выборки.
Формула в ячейке  C6 : вычисляет p-значение, связанное со статистикой теста, рассчитанной в ячейке B6  , с использованием функции Excel НОРМ.СТ.РАСП , которая возвращает кумулятивную вероятность для нормального распределения со средним значением = 0 и стандартным отклонением = 1.
Поскольку p-значение ( 0,17 ) больше, чем выбранный нами уровень значимости   0,1 , мы не можем отвергнуть нулевую гипотезу. У нас нет достаточных доказательств, чтобы сказать, что истинный процент клиентов, которые удовлетворены их обслуживанием, составляет менее 90%.

Пример 2 одновыборочного Z-теста

Телефонная компания утверждает, что 90% ее клиентов довольны их услугами. Чтобы проверить это утверждение, независимый исследователь собрал простую случайную выборку из 200 клиентов и спросил их, довольны ли они своим сервисом, на что 190 ответили утвердительно

Протестируйте нулевую гипотезу о том, что 90 % клиентов удовлетворены своим обслуживанием, и альтернативную гипотезу о том, что не 90 % клиентов удовлетворены их обслуживанием. Используйте уровень значимости 0,05.

На следующем снимке экрана показано, как выполнить двусторонний одновыборочный тест z в Excel вместе с используемыми формулами:

Вам нужно заполнить значения для ячеек B1:B3 . Затем значения для ячеек B5:B7 автоматически рассчитываются с использованием формул, показанных в ячейках C5:C7 .

Обратите внимание, что показанные формулы делают следующее:

Формула в ячейке C5 : рассчитывает долю выборки по формуле Частота / Размер выборки.

Формула в ячейке C6 : вычисляет статистику теста по формуле (p-P) / (√P(1-P) / n), где p — доля выборки, P — гипотетическая доля населения, а n — размер выборки.

Формула в ячейке C6 : вычисляет p-значение, связанное со статистикой теста, рассчитанной в ячейке B6 , с использованием функции Excel НОРМ.СТ.РАСП , которая возвращает кумулятивную вероятность для нормального распределения со средним значением = 0 и стандартным отклонением = 1. Мы умножьте это значение на два, так как это двусторонний тест.

Поскольку p-значение ( 0,018 ) меньше выбранного нами уровня значимости 0,05 , мы отклоняем нулевую гипотезу и делаем вывод, что истинный процент клиентов, удовлетворенных своим обслуживанием, не равен 90%.

Двухсторнний Z-тест в Excel

Двухсторонний Z- тест используется для проверки разницы между двумя значениями выборки.

Например, предположим, что руководитель департамента образования утверждает, что процент учащихся, которые предпочитают шоколадное молоко обычному молоку в школьных столовых, одинаков для школы 1 и школы 2.

Чтобы проверить это утверждение, независимый исследователь получает простую случайную выборку из 100 учеников из каждой школы и опрашивает их об их предпочтениях. Он обнаружил, что 70 % учеников в школе 1 предпочитают шоколадное молоко, а 68 % учащихся в школе 2 предпочитают шоколадное молоко.

Мы можем использовать двухвыборочный z-тест, чтобы проверить, одинаков ли процент учащихся, предпочитающих шоколадное молоко обычному, в обеих школах.

Алгоритм выполнения двухвыборочного Z-теста

Мы можем использовать следующие шаги для выполнения z-теста двух пропорций:

Шаг 1. Сформулируйте гипотезы.

Нулевая гипотеза (H0): P ₁ = P ₂

Альтернативная гипотеза: (Ha): P ₁ ≠ P ₂

Шаг 2. Найдите статистику теста и соответствующее значение p.

Во-первых, найдите долю объединенной выборки p:

p = (p ₁ * n ₁ + p ₂ * n ₂ ) / (n ₁ + n ₂ )

р = (0,70 * 100 + 0,68 * 100) / (100 + 100) = 0,69

Затем используйте p в следующей формуле, чтобы найти тестовую статистику z:

z = (p ₁ -p ₂ ) / √p * (1-p) * [ (1/n ₁ ) + (1/n ₂ )]

z = (0,70–0,68) / √,69 * (1–0,69) * [(1/100) + (1/100)] = 0,02 / 0,0654 = 0,306

Используйте Калькулятор Z-оценки для P-значения с az-оценкой 0,306 и двусторонним тестом, чтобы найти, что p-значение = 0,759 .

Шаг 3. Отклонить или не отклонить нулевую гипотезу.

Во-первых, нам нужно выбрать уровень значимости для теста. Обычно выбираются значения 0,01, 0,05 и 0,10. Для этого примера возьмем 0,05. Поскольку p-значение не меньше нашего уровня значимости 0,05, мы не можем отвергнуть нулевую гипотезу.

Таким образом, у нас нет достаточных оснований утверждать, что процент учащихся, предпочитающих шоколадное молоко, различен для школы 1 и школы 2.

Пример Z-теста с двумя выборками (двухсторонний)

Руководитель школьного округа утверждает, что процент учащихся, которые предпочитают шоколадное молоко обычному молоку в школьных столовых, одинаков для школы 1 и школы 2.

Основываясь на этих результатах, можем ли мы отвергнуть утверждение директора школы о том, что процент учащихся, предпочитающих шоколадное молоко, одинаков для школ 1 и 2? Используйте уровень значимости 0,05.

На следующем снимке экрана показано, как выполнить двусторонний тест Z с двумя выборками в Excel вместе с используемыми формулами:

Вам нужно заполнить значения для ячеек B1:B4 . Затем значения для ячеек B6:B8 автоматически рассчитываются с использованием формул, показанных в ячейках C6:C8 .

Обратите внимание, что показанные формулы делают следующее:

Формула в ячейке C6 : рассчитывает долю объединенной выборки по формуле p = (p ₁ * n ₁ + p ₂ * n ₂ ) / (n ₁ + n ₂ )

Формула в ячейке C7 : вычисляет тестовую статистику z по формуле z = (p ₁ -p ₂ ) / √p * (1-p) * [ (1/n ₁ ) + (1/n ₂ )], где p - доля объединенной выборки.

Формула в ячейке C8 : вычисляет значение p, связанное со статистикой теста, рассчитанной в ячейке B7 , с использованием функции Excel НОРМ.СТ.РАСП , которая возвращает кумулятивную вероятность для нормального распределения со средним значением = 0 и стандартным отклонением = 1. Мы умножьте это значение на два, так как это двусторонний тест.

Поскольку p-значение ( 0,759 ) не меньше выбранного нами уровня значимости 0,05 , мы не можем отвергнуть нулевую гипотезу. Таким образом, у нас нет достаточных оснований утверждать, что процент учащихся, предпочитающих шоколадное молоко, различен для школы 1 и школы 2.

Z-Тест с двумя выборками

Руководитель школьного округа утверждает, что процент учащихся, которые предпочитают шоколадное молоко обычному молоку в школе 1, меньше или равен проценту в школе 2.

Основываясь на этих результатах, можем ли мы отвергнуть утверждение директора школы о том, что процент учащихся, предпочитающих шоколадное молоко, в школе 1 меньше или равен проценту учеников в школе 2? Используйте уровень значимости 0,05.

Двухвыборочный z-тест в Excel:

Нужно заполнить значения для ячеек B1:B4 . Затем значения для ячеек B6:B8 автоматически рассчитываются с использованием формул, показанных в ячейках C6:C8 . Обратите внимание, что показанные формулы выполняют следующее:

Формула в ячейке C6 : рассчитывает долю объединенной выборки по формуле p = (p ₁ * n ₁ + p ₂ * n ₂ ) / (n ₁ + n ₂ )

Формула в ячейке C8 : вычисляет p-значение, связанное со статистикой теста, рассчитанной в ячейке B7 , с использованием функции Excel НОРМ.СТ.РАСП , которая возвращает кумулятивную вероятность для нормального распределения со средним значением = 0 и стандартным отклонением = 1.

Поскольку p-значение ( 0,379 ) не меньше выбранного нами уровня значимости 0,05 , мы не можем отвергнуть нулевую гипотезу. Таким образом, у нас нет достаточных оснований утверждать, что процент учащихся, предпочитающих шоколадное молоко, в школе 2 больше, чем в школе 1.

Последнее изменение: Понедельник, 2 июня 2025, 13:35